《2025年春如金卷课时同步ABC九年级数学上册北师大版》

9. 如图，四边形 $ABCD$ 是菱形，$\angle ACD = 30^{\circ}$，$BD = 6$.求：
(1)$\angle BAD$ 的度数和 $AB$，$AC$ 的长；
(2)$DH\perp BC$，求 $DH$ 的长.

答案：
(1)
∵四边形ABCD是菱形，
∴AB=BC=CD=AD，AC⊥BD，AC平分∠BCD，∠BAD+∠BCD=180°。
∵∠ACD=30°，
∴∠BCD=2∠ACD=60°，
∴∠BAD=180°-60°=120°。
设AC与BD交于点O，则BO=OD=BD/2=3，AC⊥BD，∠DOC=90°。
在Rt△DOC中，∠OCD=30°，OD=3，
∴CD=2OD=6（30°角所对直角边是斜边一半），
∴AB=CD=6。
OC=√(CD²-OD²)=√(6²-3²)=3√3，
∴AC=2OC=6√3。
(2)
菱形ABCD面积S=AC·BD/2=6√3×6/2=18√3。
又S=BC·DH，BC=AB=6，
∴6·DH=18√3，
∴DH=3√3。
(1)∠BAD=120°，AB=6，AC=6√3；
(2)DH=3√3。

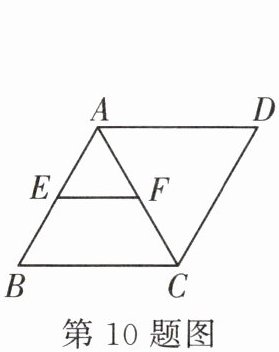
10. 如图，在菱形 $ABCD$ 中，$E$，$F$ 分别是 $AB$，$AC$ 的中点，若 $EF = 3$，则菱形 $ABCD$ 的周长为（ ）

A.24
B.18
C.12
D.9

答案： A

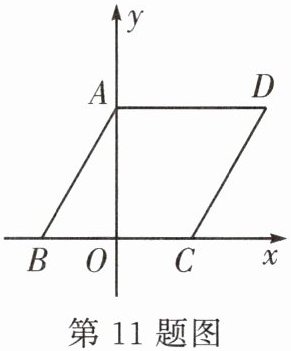
11. 如图，在平面直角坐标系中，菱形 $ABCD$ 的顶点 $A$，$B$，$C$ 在坐标轴上.若点 $B$ 的坐标为 $(-1,0)$，$\angle BCD = 120^{\circ}$，则点 $D$ 的坐标为（ ）

A.$(2,2)$
B.$(\sqrt{3},2)$
C.$(3,\sqrt{3})$
D.$(2,\sqrt{3})$

答案： D

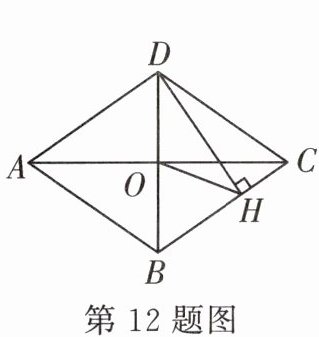
12. 如图，菱形 $ABCD$ 的对角线 $AC$，$BD$ 相交于点 $O$，过点 $D$ 作 $DH\perp BC$，垂足为点 $H$，连接 $OH$.若 $OA = 4$，$S_{菱形ABCD} = 24$，则 $OH$ 的长为______.

答案： 3

13. 如图，在平面直角坐标系中，菱形 $ABCD$ 对角线的交点坐标是 $O(0,0)$，点 $B$ 的坐标是 $(0,1)$，且 $BC = \sqrt{5}$，则点 $A$ 的坐标是______.

答案： (2,0)

14. 如图，在菱形 $ABCD$ 中，点 $E$，$F$ 分别是 $AD$，$DC$ 的中点，连接 $EF$ 并延长，交 $BC$ 的延长线于点 $G$，连接 $AC$.
(1) 求证：四边形 $ACGE$ 是平行四边形；
(2) 连接 $AG$，若 $\angle FGC = 60^{\circ}$，$AB = 4$，求 $AG$ 的长.

答案：
(1) 见证明；
(2) AG=2√3。