《2025年春如金卷课时同步ABC九年级数学上册北师大版》

7. 下列方程：①$3x^{2}+x = 20$；②$2x^{2}-3x + 4 = 0$；③$x^{2}-\frac{1}{x}=4$；④$x^{2}=1$；⑤$x^{2}-3x + 3 = 0$中，一元二次方程有（ ）

A.$2$个
B.$3$个
C.$4$个
D.$5$个

答案： C

8. 某学校为了进行劳动教育，开辟了一个面积为$130$m$^{2}$的矩形种植园，打算一面利用长为$15$m的仓库墙面，其他三面利用长为$33$m的围栏。如图，如果设矩形与墙面垂直的一边长为$x$m，那么下列方程符合题意的是（ ）

A.$x(33 - 2x)=130$
B.$x(15 - x)=130$

C.$x(15 - 2x)=130$
D.$x(33 - x)=130$

答案： A

9. 根据题意列出方程：
(1)两个连续偶数的平方和是$100$，求这两个数。若设较小的数为$x$，则可列方程为____；
(2)某中学准备建一个面积为$375$m$^{2}$的矩形游泳池，且游泳池的宽比长短$10$m。若设游泳池的长为$x$m，则可列方程为____；
(3)生物兴趣小组的学生，将自己收集的标本向本组其他成员各赠送一件，全组共互赠了$132$件，如果全组共有$x$名同学，那么根据题意列出的方程是____。

答案：
(1) $x^2 + (x + 2)^2 = 100$
(2) $x(x - 10) = 375$
(3) $x(x - 1) = 132$

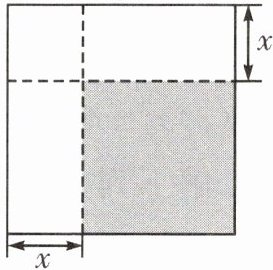
10. 如图，将边长为$12$的正方形纸片，沿两边各剪去一个一边长为$x$的长方形，剩余的部分（阴影部分）面积为$64$，根据条件，列出方程，并化为一般式。

答案： $x^2 - 24x + 80 = 0$

11. 如图，四边形$ACDE$是证明勾股定理时用到的一个图形，$a,b,c$是$Rt\triangle ABC$和$Rt\triangle BED$边长，易知$AE=\sqrt{2}c$，这时我们把关于$x$的形如$ax^{2}+\sqrt{2}cx + b = 0$的一元二次方程称为“勾系一元二次方程”，比如$3x^{2}+5\sqrt{2}x + 4 = 0$是“勾系一元二次方程”。请解决下列问题：
(1)试判断方程$x^{2}+2x + 1 = 0$____“勾系一元二次方程”（填“是”或“不是”）；
(2)若$x = - 1$是“勾系一元二次方程”$ax^{2}+\sqrt{2}cx + b = 0$的一个根，且四边形$ACDE$的周长是$12$，求$\triangle ABC$面积。

答案：
(1) 是；
(2) 2