《2025年春如金卷课时同步ABC九年级数学上册北师大版》

6. 如图，在△ABC中，∠B=60°，AB=6，AC=8.将△ABC沿图中的DE剪开.剪下的阴影三角形与原三角形不相似的是（ ）


A.
B.
C.
D.

答案： C

7. 如图，在△ABC中，点D是AB边上的一点，当∠ADC=∠______时，△ABC与△ACD相似.

答案： ACB

8. 如图，在纸板△ABC中，AC=8，BC=4，AB=10，点P是AC上一点，过点P沿直线剪下一个与△ABC相似的小三角形纸板.如果有4种不同的剪法，那么AP长的取值范围是______.

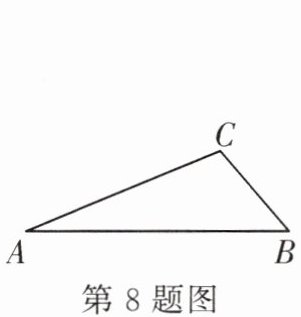
答案： 6＜AP＜8

9. 如图，在□ABCD中，过点A作AE⊥BC，垂足为点E，连接DE，点F为线段DE上一点，且∠AFE=∠B.
(1)求证：△ADF∽△DEC；
(2)若AB=8，AD=6√{3}，AF=4√{3}，求DE的长.

答案：
(1) 证明：
由题意，四边形 $ABCD$ 为平行四边形，
$\therefore AD // BC, AB // CD$，
$\therefore \angle ADF = \angle DEC$（两直线平行，内错角相等），
已知 $\angle AFE = \angle B$，
在平行四边形 $ABCD$ 中，$\angle B + \angle BCD = 180°$（平行四边形的邻角互补），
$\angle AFC + \angle AFE = 180°$，
$\therefore \angle AFC = \angle BCD$，
$\therefore \angle AFD = \angle DCE$，
在 $\triangle ADF$ 和 $\triangle DEC$ 中，
$\angle ADF = \angle DEC$，
$\angle AFD = \angle DCE$，
$\therefore \triangle ADF \sim \triangle DEC$（AA 相似）。
(2)
$\because$四边形 $ABCD$ 为平行四边形，
$\therefore CD = AB = 8$，
由
(1) 可知 $\triangle ADF \sim \triangle DEC$，
$\therefore\frac{AD}{DE} = \frac{AF}{CD}$，
$\therefore DE = \frac{AD \cdot CD}{AF} = \frac{6\sqrt{3} × 8}{4\sqrt{3}} = 12$。

10. 四边形的一条对角线把这个四边形分成两个三角形，如果这两个三角形相似(不全等)，我们就把这条对角线称为这个四边形的“理想对角线”.
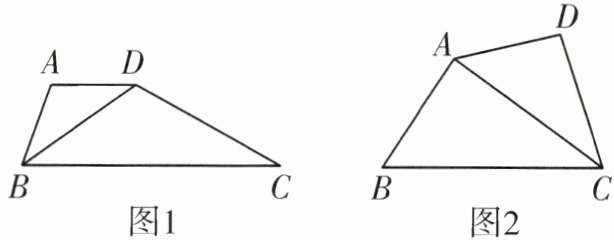
(1)如图1，在四边形ABCD中，∠ABC=70°，AB=AD，AD//BC，当∠ADC=145°时.求证：对角线BD是四边形ABCD的“理想对角线”.
(2)如图2，四边形ABCD中，AC平分∠BCD，当∠BCD与∠BAD满足什么关系时，对角线AC是四边形ABCD的“理想对角线”，请说明理由.

答案：
(1) 证明：
∵AD//BC，
∴∠ADB=∠DBC（设为∠1）.
∵AB=AD，
∴∠ABD=∠ADB=∠1.
∵AD//BC，
∴∠BAD+∠ABC=180°，∠ABC=70°，
∴∠BAD=110°.
在△ABD中，∠BAD=180°-2∠1=110°，解得∠1=35°，
∴∠ABD=∠ADB=∠DBC=35°.
∵∠ADC=145°，
∴∠BDC=∠ADC-∠ADB=145°-35°=110°.
在△DBC中，∠BCD=180°-∠DBC-∠BDC=180°-35°-110°=35°.
∴∠ABD=∠DBC=35°，∠BAD=∠BDC=110°，∠ADB=∠BCD=35°.
∴△ABD∽△DBC（AA）.
∵AB=AD≠BC（否则全等），
∴不全等.
∴BD是“理想对角线”.
(2) 当∠BCD+2∠BAD=360°时，AC是“理想对角线”.
理由：
∵AC平分∠BCD，设∠ACB=∠ACD=α，则∠BCD=2α.
若△ABC∽△CAD，则∠ABC=∠CAD，∠BAC=∠ADC，∠ACB=∠ACD=α.
在△ABC中，∠ABC+∠BAC+α=180°；在△CAD中，∠CAD+∠ADC+α=180°.
设∠ABC=∠CAD=x，∠BAC=∠ADC=y，则x+y=180°-α.
∠BAD=∠BAC+∠CAD=x+y=180°-α.
∵α=∠BCD/2，
∴∠BAD=180°-∠BCD/2，即∠BCD+2∠BAD=360°.
此时△ABC∽△CAD且不全等，
∴AC是“理想对角线”.
答案
(1) 见解析；
(2) ∠BCD+2∠BAD=360°，理由见解析.