《2025年春如金卷课时同步ABC九年级数学上册北师大版》

1. 两角分别对应______的两个三角形相似；两边______且夹角______的两个三角形相似；三边______的两个三角形相似；相似三角形的对应边______，对应角______.

答案： 相等；对应成比例；相等；对应成比例；成比例；相等

2. 如图，在$\triangle ABC$中，$DE// BC$，且$AD:DB = 2:1$，那么$DE:BC =$（ ）

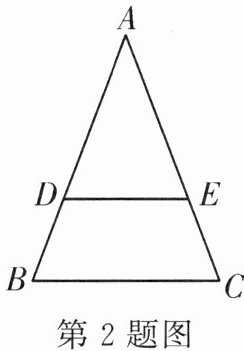
A.$2:1$
B.$1:2$
C.$3:2$
D.$2:3$

答案： D

3. 如图，$E$是$□ ABCD$边$CD$延长线上一点，$BE$交$AD$于$F$，则图中的相似三角形共有（ ）

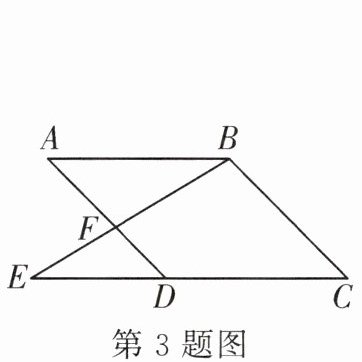
A.$4$对
B.$3$对
C.$2$对
D.$1$对

答案： B

4. 如图，$DE// BC$，$EF// AB$，则下列比例式错误的是（ ）

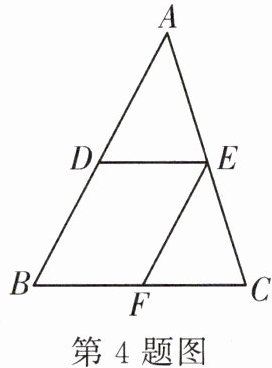
A.$\frac{AD}{AB}=\frac{AE}{AC}$
B.$\frac{CE}{CF}=\frac{EA}{FB}$
C.$\frac{DE}{BC}=\frac{AD}{BD}$
D.$\frac{EF}{AB}=\frac{CF}{CB}$

答案： C

5. 如图，$D$是$\triangle ABC$的边$AB$上的一点，那么下列四个条件不能单独判定$\triangle ABC\backsim\triangle ACD$的是（ ）

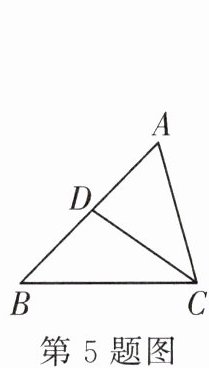
A.$\angle B=\angle ACD$
B.$\angle ADC=\angle ACB$
C.$\frac{AC}{CD}=\frac{AB}{BC}$
D.$AC^{2}=AD\cdot AB$

答案： C

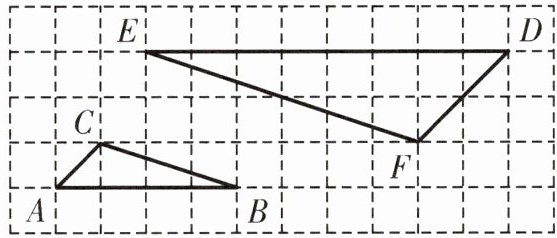
6. 如图的网格图中每个方格都是边长为$1$的正方形，求证：$\triangle ABC\backsim\triangle DEF$.

答案： 证明：
1. 计算△ABC各边长：
$ AB $: 横向3格，$ AB = 3 $.
$ AC $: 纵向1格、横向1格，由勾股定理得 $ AC = \sqrt{1^2 + 1^2} = \sqrt{2} $.
$ BC $: 纵向1格、横向2格，由勾股定理得 $ BC = \sqrt{1^2 + 2^2} = \sqrt{5} $.
2. 计算△DEF各边长：
$ DE $: 横向6格，$ DE = 6 $.
$ DF $: 纵向2格、横向2格，由勾股定理得 $ DF = \sqrt{2^2 + 2^2} = 2\sqrt{2} $.
$ EF $: 纵向2格、横向4格，由勾股定理得 $ EF = \sqrt{2^2 + 4^2} = 2\sqrt{5} $.
3. 验证三边成比例：
$ \frac{AB}{DE} = \frac{3}{6} = \frac{1}{2} $，
$ \frac{AC}{DF} = \frac{\sqrt{2}}{2\sqrt{2}} = \frac{1}{2} $，
$ \frac{BC}{EF} = \frac{\sqrt{5}}{2\sqrt{5}} = \frac{1}{2} $.
因此，$ \frac{AB}{DE} = \frac{AC}{DF} = \frac{BC}{EF} $.
4. 结论：
由“三边成比例的两个三角形相似”，得 $ \triangle ABC \backsim \triangle DEF $.
证毕.