《2025年课堂点睛八年级数学上册华师大版》

1. 在$\triangle ABC$中,已知$\angle A = 32^{\circ}$,$\angle C = 58^{\circ}$,则$\angle B = $90$^{\circ}$,此三角形是直角三角形。

答案： 90 直角

2. 在下列条件中,①$\angle A = 90^{\circ}-\angle B$,②$\angle A= \angle B = 2\angle C$,③$\angle A:\angle B:\angle C = 5:3:2$,④$\angle A+\angle B= \angle C$,能判定$\triangle ABC$为直角三角形的有①③④(填序号)。

答案： ①③④

3. (沈丘县期末)以下列各组数为边长,能构成直角三角形的是(B)
A.$4$,$5$,$6$
B.$1$,$1$,$\sqrt{2}$
C.$6$,$8$,$11$
D.$5$,$12$,$23$

答案： B

4. (教材第 132 页习题第 5 题改编)在$\triangle ABC$中,$\angle A$,$\angle B$,$\angle C的对边分别为a$,$b$,$c$,且$a^{2}= b^{2}-c^{2}$,则下列说法正确的是(B)
A.$\angle A = 90^{\circ}$
B.$\angle B = 90^{\circ}$
C.$\angle C = 90^{\circ}$
D.$\angle A＞90^{\circ}$

答案： B

5. (渝北区期末)如图,在$\triangle ABC$中,$BC = 8$,$\angle A = 45^{\circ}$,点$D是AC$边上一点,连结$BD$,若$CD = 6$,$BD = 10$,则线段$AD= $2。

答案： 2

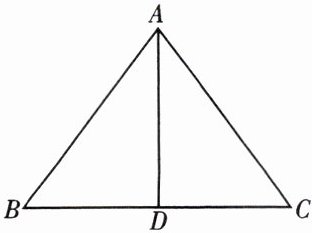
6. 如图,在$\triangle ABC$中,$AB = 5$,$BC = 6$,$BC边上的中线AD = 4$。
(1)$AD与BC$互相垂直吗？为什么？
(2)求$AC$的长。

答案：
(1)解:AD 与 BC 互相垂直,理由如下:
∵AB=5,BC=6,BC 边上的中线 AD=4,
∴BD=3,
∵3²+4²=5²,
∴∠ADB=∠ADC=90°,
∴AD⊥BC,即 AD 与 BC 互相垂直.
(2)在 Rt△ADC 中,AC=√(AD²+CD²)=√(4²+3²)=5.

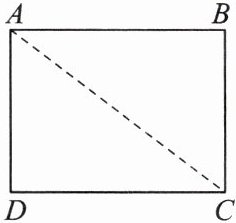
7. 如图是一农民建房时挖的地基的平面图,标准地基为长方形,挖完后测得$AB = CD = 8m$,$AD = BC = 6m$,对角线$AC = 9.2m$,请你帮他判断一下挖的地基是否合格,并说明理由。

答案： 解:不合格.理由如下:
∵AB=DC=8m,AD=BC=6m,
∴AB²+BC²=8²+6²=64+36=100.
∵AC²=9.2²=84.64,
∴AB²+BC²≠AC².
∴∠ABC≠90°,即该农民挖的地基不合格.

8. 下面几组数中,为勾股数的一组是(B)
A.$4$,$5$,$6$
B.$12$,$16$,$20$
C.$-10$,$24$,$26$
D.$2.4$,$4.5$,$5.1$

答案： B

9. 下列几组数：①$9$,$12$,$15$；②$8$,$15$,$17$；③$7$,$24$,$25$；④$n^{2}-1$,$2n$,$n^{2}+1$($n是大于1$的整数)。其中是勾股数的有(D)
A.$1$组
B.$2$组
C.$3$组
D.$4$组

答案： D

10. 下列各组数为勾股数的是①。
①$6$,$8$,$10$；②$7$,$8$,$10$；③$\frac{3}{5}$,$\frac{4}{5}$,$1$。

答案： ①

11. (成都西川中学单元卷)如图,在单位正方形组成的网格图中标有$AB$,$CD$,$EF$,$GH$四条线段,其中能构成一个直角三角形三边的线段是(B)

A.$CD$,$EF$,$GH$
B.$AB$,$EF$,$GH$
C.$AB$,$CD$,$GH$
D.$AB$,$CD$,$EF$

答案： B