《2025年课堂点睛八年级数学上册华师大版》

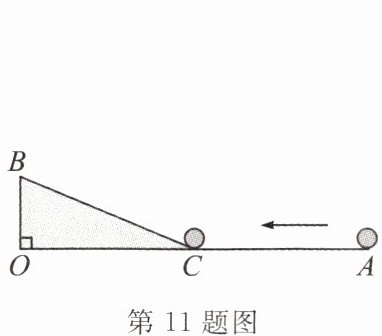
11. 【跨学科】如图,$\angle AOB = 90°$,$OA = 25m$,$OB = 5m$,一机器人在点 B 处看见一个小球从点 A 出发沿着 AO 方向匀速滚向点 O,机器人立即从点 B 出发,沿直线匀速前进拦截小球,恰好在点 C 处截住了小球. 如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程 BC 是13m.

答案： 13

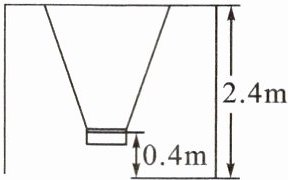
12. 如图,小红荡秋千,秋千架高 2.4m,秋千座位离地 0.4m,小红荡起最高时,座位离地 0.8m. 此时小红荡出的水平距离(荡到秋千架两边的最高点之间的距离)是多少？

答案：
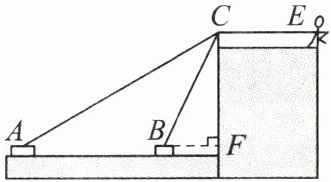
解:如图为秋千侧面图， 座位最低点为A,最高点为B,则OA=OB=2.4 - 0.4 =2(m).过点B作OA的垂线,垂足为点C,则AC=0.8 - 0.4=0.4 (m),OC=2 - 0.4=1.6(m).在Rt△OCB中,由勾股定理，得BC=√(OB² - OC²)=√(2² - 1.6²)=1.2 (m),所以2BC=2×1.2=2.4 (m).故小红荡出的水平距离是2.4m.

13. 如图,一条绷紧的绳索一端系着一艘小船. 河岸上一男孩拽着绳子另一端向右走,绳端从 C 移动到 E,同时小船从 A 移动到 B,且绳长始终保持不变. 回答下列问题：
(1)AC=(选填“＞”“＜”或“=”)$BC + CE$；
(2)若 $CF = 5m$,$AF = 12m$,$AB = 9m$,$CE // AB$,求男孩向右移动的距离.(结果保留根号)

答案：
(1)=　
(2)解:在Rt△CFA中,由勾股定理，得AC=√(AF² + CF²)=13m,
∵AF=12m,AB=9m,
∴BF =AF - AB=12 - 9=3(m),在Rt△CFB中,由勾股定理,得BC=√(CF² + BF²)=√(5² + 3²)=√34 (m),
∴CE=AC - BC=(13 - √34)m,
∴男孩向右移动的距离为(13 - √34)m.

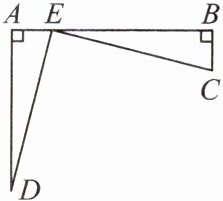
14. 【核心素养·应用意识】某市决定在相距 10km 的 A,B 两地之间的 E 点修建一个土特产加工基地,如图所示,有 C,D 两个农庄,且 $DA \perp AB$ 于点 A,$CB \perp AB$ 于点 B,已知 $DA = 8km$,$BC = 2km$,要使 C,D 两农庄到基地的距离相等,那么基地 E 应建在距离 A 地多远的地方？

答案： 解:
∵C,D两个农庄到基地E的距离相等,
∴CE=DE.在Rt△CBE 和Rt△DAE中,由勾股定理，得CE²=BE² + BC²,DE²=AD² + AE²,即BE² + BC²=AD² + AE²,设AE=xkm,则BE=(10 - x)km.
∴(10 - x)² + 2²=8² + x²,解得x=2,
∴基地E应建在距离A 地2km的地方.