第81页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
1.$\sqrt{(\tan 30^{\circ}-1)^2}$的值是
$1-\frac{\sqrt{3}}{3}$
.
答案:
$1-\frac{\sqrt{3}}{3}$
2.在$\triangle ABC$中,$\angle C=90^{\circ}$,$AC=m$.若$\angle A=\alpha$,则$AB$的长为
$\frac{m}{\cos \alpha}$
.
答案:
$\frac{m}{\cos \alpha}$
3.如图所示,某商场准备将自动扶梯改造成斜坡式.若商场的层高$AB$为$6\operatorname{m}$,$\angle ACB$为$45^{\circ}$,改造后扶梯$AD$的坡度是$1:2$,则改造后扶梯$AD$相比改造前$AC$增加的长度是
$\operatorname{m}$.

$(6\sqrt{5}-6\sqrt{2})$
$\operatorname{m}$.

答案:
$(6\sqrt{5}-6\sqrt{2})$
4.若等腰三角形一腰上的高与腰长之比是$1:2$,则该等腰三角形顶角的大小为
$30^{\circ}$或$150^{\circ}$
.
答案:
$30^{\circ}$或$150^{\circ}$
5.如图①所示,将正方形纸片$ABCD$对折,使$AB$与$CD$重合,折痕为$EF$.如图②所示,将纸片展开后再折叠一次,使点$C$与点$E$重合,折痕为$GH$,点$B$的对应点为点$M$,$EM$交$AB$于点$N$,则$\tan\angle ANE=$

$\frac{3}{4}$
.
答案:
$\frac{3}{4}$
6.计算.
(1)$(-1)^2-2\cos30^{\circ}+\sqrt{3}+(-2024)^0$;
(2)$\frac{3\tan30^{\circ}-2\tan60^{\circ}}{\cos60^{\circ}}+4\sin60^{\circ}$.
(1)$(-1)^2-2\cos30^{\circ}+\sqrt{3}+(-2024)^0$;
(2)$\frac{3\tan30^{\circ}-2\tan60^{\circ}}{\cos60^{\circ}}+4\sin60^{\circ}$.
答案:
1. 计算$(-1)^2 - 2\cos30^{\circ}+\sqrt{3}+(-2024)^0$:
解:
根据幂的运算:$(-1)^2 = 1$,$(-2024)^0 = 1$($a^0 = 1,a\neq0$);
根据特殊三角函数值:$\cos30^{\circ}=\frac{\sqrt{3}}{2}$。
则$(-1)^2 - 2\cos30^{\circ}+\sqrt{3}+(-2024)^0$
$=1-2×\frac{\sqrt{3}}{2}+\sqrt{3}+1$
$=1 - \sqrt{3}+\sqrt{3}+1$
$=2$。
2. 计算$\frac{3\tan30^{\circ}-2\tan60^{\circ}}{\cos60^{\circ}}+4\sin60^{\circ}$:
解:
根据特殊三角函数值:$\tan30^{\circ}=\frac{\sqrt{3}}{3}$,$\tan60^{\circ}=\sqrt{3}$,$\cos60^{\circ}=\frac{1}{2}$,$\sin60^{\circ}=\frac{\sqrt{3}}{2}$。
则$\frac{3\tan30^{\circ}-2\tan60^{\circ}}{\cos60^{\circ}}+4\sin60^{\circ}$
$=\frac{3×\frac{\sqrt{3}}{3}-2×\sqrt{3}}{\frac{1}{2}}+4×\frac{\sqrt{3}}{2}$
$=\frac{\sqrt{3}-2\sqrt{3}}{\frac{1}{2}} + 2\sqrt{3}$
$=\frac{-\sqrt{3}}{\frac{1}{2}}+2\sqrt{3}$
$=-2\sqrt{3}+2\sqrt{3}$
$=0$。
综上,(1)的结果为$2$;(2)的结果为$0$。
解:
根据幂的运算:$(-1)^2 = 1$,$(-2024)^0 = 1$($a^0 = 1,a\neq0$);
根据特殊三角函数值:$\cos30^{\circ}=\frac{\sqrt{3}}{2}$。
则$(-1)^2 - 2\cos30^{\circ}+\sqrt{3}+(-2024)^0$
$=1-2×\frac{\sqrt{3}}{2}+\sqrt{3}+1$
$=1 - \sqrt{3}+\sqrt{3}+1$
$=2$。
2. 计算$\frac{3\tan30^{\circ}-2\tan60^{\circ}}{\cos60^{\circ}}+4\sin60^{\circ}$:
解:
根据特殊三角函数值:$\tan30^{\circ}=\frac{\sqrt{3}}{3}$,$\tan60^{\circ}=\sqrt{3}$,$\cos60^{\circ}=\frac{1}{2}$,$\sin60^{\circ}=\frac{\sqrt{3}}{2}$。
则$\frac{3\tan30^{\circ}-2\tan60^{\circ}}{\cos60^{\circ}}+4\sin60^{\circ}$
$=\frac{3×\frac{\sqrt{3}}{3}-2×\sqrt{3}}{\frac{1}{2}}+4×\frac{\sqrt{3}}{2}$
$=\frac{\sqrt{3}-2\sqrt{3}}{\frac{1}{2}} + 2\sqrt{3}$
$=\frac{-\sqrt{3}}{\frac{1}{2}}+2\sqrt{3}$
$=-2\sqrt{3}+2\sqrt{3}$
$=0$。
综上,(1)的结果为$2$;(2)的结果为$0$。
7.如图所示,网格中的每个小正方形的边长均为$1$,端点$A$,$B$均在小正方形的顶点上.
(1)在图中画出平行四边形$ABCD$,点$C$和点$D$均在小正方形的顶点上,且平行四边形的面积为$12$.
(2)在图中画出以$AB$为腰的等腰$Rt\triangle ABE$,且点$E$在小正方形的顶点上.
(3)连接$DE$,直接写出$\angle CDE$的正切值.

(1)在图中画出平行四边形$ABCD$,点$C$和点$D$均在小正方形的顶点上,且平行四边形的面积为$12$.
(2)在图中画出以$AB$为腰的等腰$Rt\triangle ABE$,且点$E$在小正方形的顶点上.
(3)连接$DE$,直接写出$\angle CDE$的正切值.

答案:
解:(1)如图,四边形 $ABCD$ 即为所求.
(2)如图,$\triangle ABE$ 即为所求.
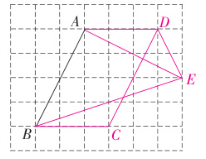
(3)$\angle CDE$ 的正切值为 $\frac{4}{3}$.
解:(1)如图,四边形 $ABCD$ 即为所求.
(2)如图,$\triangle ABE$ 即为所求.

(3)$\angle CDE$ 的正切值为 $\frac{4}{3}$.
8.如图所示,工程队修公路时遇到一座小山,需要修一条隧道,为了加快施工进度,计划在小山的另一侧同时施工.为了使小山的另一侧的开挖点$C$在$AB$的延长线上,设过点$C$作直线$AB$的垂线$l$,过点$B$作一直线(从小山的旁边经过)与$l$相交于点$D$,经测量$\angle ABD=135^{\circ}$,$BD=800\operatorname{m}$,求应该在直线$l$上距离$D$点多远的$C$处开挖.(结果保留根号)
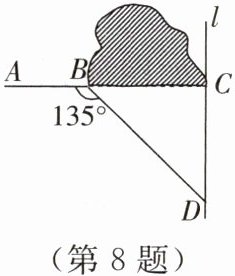

答案:
解:
∵$\angle ABD=135^{\circ}$,
$\angle ABC=180^{\circ}$,
∴$\angle CBD=45^{\circ}$.
又
∵$CD\perp BC$,
即$\angle ACD=90^{\circ}$,
∴$CD=BD· \sin 45^{\circ}=800× \frac{\sqrt{2}}{2}=400\sqrt{2}$(m).
故应该在直线 $l$ 上距离 $D$ 点 $400\sqrt{2}$ m 的 $C$ 处开挖.
∵$\angle ABD=135^{\circ}$,
$\angle ABC=180^{\circ}$,
∴$\angle CBD=45^{\circ}$.
又
∵$CD\perp BC$,
即$\angle ACD=90^{\circ}$,
∴$CD=BD· \sin 45^{\circ}=800× \frac{\sqrt{2}}{2}=400\sqrt{2}$(m).
故应该在直线 $l$ 上距离 $D$ 点 $400\sqrt{2}$ m 的 $C$ 处开挖.
查看更多完整答案,请扫码查看


