《2025年作业本江西教育出版社九年级数学全一册北师大版》

21. 模具厂计划生产面积为 9、周长为$m$的矩形模具. 对于$m$的取值范围,小明已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下：
(1)建立函数模型
设矩形相邻两边的长分别为$x,y$,由矩形的面积为 9, 得$xy=9$,即$y=\frac{9}{x}$; 由周长为$m$, 得$2(x+y)=m$,即$y=-x+\frac{m}{2}$.满足要求的$(x, y)$应是两个函数图象在第一象限内交点的坐标.
(2)画出函数图象
函数$y=\frac{9}{x}(x＞0)$的图象如图所示,而函数$y=-x+\frac{m}{2}$的图象可由直线$y=-x$平移得到.请在同一平面直角坐标系中直接画出直线$y=-x$.
(3)平移直线$y=-x$, 观察函数图象
①当直线平移到与函数$y=\frac{9}{x}(x＞0)$的图象有唯一交点$(3,3)$时, 周长$m$的值为12.
②在直线平移的过程中, 交点的个数还有哪几种情况? 请写出交点个数及对应的周长$m$的取值范围.
(4)得出结论
若能生产出面积为 9 的矩形模具, 则周长$m$的取值范围为$m\geqslant12$.

答案：
21.
-
(1) 因为$x$、$y$表示矩形的边长，所以$x\gt0$，$y\gt0$，所以交点在第一象限；
(2)如图所示

-
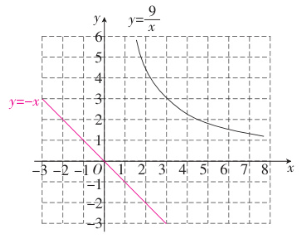
(3) ① 当交点为$(3,3)$时，代入$y=-x+\frac{m}{2}$，得$3=-3+\frac{m}{2}$，解得$m = 12$；
② 联立$y=\frac{9}{x}$与$y=-x+\frac{m}{2}$，得$\frac{9}{x}=-x+\frac{m}{2}$，整理得$x^{2}-\frac{m}{2}x + 9 = 0$，判别式$\Delta=\left(\frac{m}{2}\right)^{2}-36$。
当$\Delta\lt0$，即$\left(\frac{m}{2}\right)^{2}-36\lt0$，$m^{2}\lt144$，$0\lt m\lt12$时，无交点；
当$\Delta = 0$，即$m = 12$时，有一个交点；
当$\Delta\gt0$，即$m\gt12$时，有两个交点；
-
(4) 因为矩形存在，所以$m\geqslant12$。