《2025年作业本江西教育出版社九年级数学全一册北师大版》

1.如图所示，若$\triangle ABC$的三个顶点均在格点上，则$\cos A$的值为$\frac{2}{5}\sqrt{5}$.

答案： 设小正方形边长为$1$，延长$AB$，过$C$作$CE\perp AB$延长线于$E$。
$AE = 4$，$CE = 2$，$AC=\sqrt{4^{2}+2^{2}}=\sqrt{16 + 4}=\sqrt{20} = 2\sqrt{5}$，$AB=\sqrt{2^{2}+1^{2}}=\sqrt{5}$。
$\cos A=\frac{AE}{AC}=\frac{4}{2\sqrt{5}}=\frac{2\sqrt{5}}{5}$）。

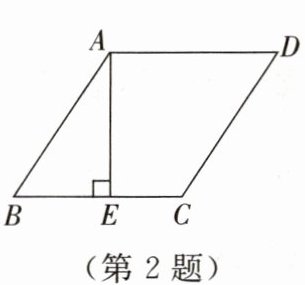
2.如图所示，在菱形$ABCD$中，$AE \perp BC$于点$E$.若$EC = 4,\sin B = \frac { 4 } { 5 }$，则菱形$ABCD$的周长是$40$.

答案： $40$

3.在$Rt \triangle ABC$中，$\angle C = 90 ^ { \circ }$.若$AB = 13,AC = 12$，则$\cos A =$$\frac{12}{13}$.

答案： $\frac{12}{13}$

4.比较$\sin 70 ^ { \circ },\cos 40 ^ { \circ },\cos 50 ^ { \circ }$的大小：
$\sin 70^{\circ} ＞ \cos 40^{\circ} ＞ \cos 50^{\circ}$(用“$＞$”连接).

答案： $\sin 70^{\circ} ＞ \cos 40^{\circ} ＞ \cos 50^{\circ}$

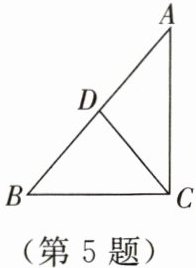
5.如图所示，在$\triangle ABC$中，$\angle ACB = 90 ^ { \circ }$，$D$为$AB$的中点，连接$CD$.若$BC = 4,CD = 3$，则$\cos \angle DCB$的值为$\frac{2}{3}$.

答案： $\frac{2}{3}$

6.在$Rt \triangle ABC$中，$\angle C = 90 ^ { \circ }$，$AB = 2BC$，求$\sin B$的值.

答案：
∵ $AB = 2BC$,
∴ $AC = \sqrt{(2BC)^2 - BC^2} = \sqrt{3}BC$.
∴ $\sin B = \frac{AC}{AB} = \frac{\sqrt{3}BC}{2BC} = \frac{\sqrt{3}}{2}$.

7.如图所示，在$Rt \triangle ABC$中，$\angle BCA = 90 ^ { \circ }$，$CD$是斜边$AB$上的高，$CD = 3$，$BD = 2$，求$\cos A$的值.

答案： 解：
∵ $\angle ACB = 90°$,
∴ $\angle B + \angle A = 90°$.
∵ $CD \perp AB$,
∴ $\angle CDA = 90°$.
∴ $\angle B + \angle BCD = 90°$.
∴ $\angle BCD = \angle A$.
∵ $CD = 3, BD = 2$,
∴ $BC = \sqrt{13}$.
∴ $\cos A = \cos \angle BCD = \frac{CD}{BC} = \frac{3}{\sqrt{13}} = \frac{3\sqrt{13}}{13}$.

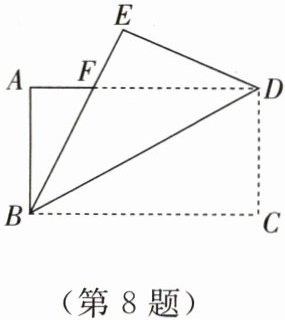
8.如图所示，将矩形$ABCD$沿对角线$BD$折叠，点$C$落在点$E$处，$BE$与$AD$相交于点$F$.
(1)求证：$\triangle BFD$是等腰三角形.
(2)若$BC = 4,CD = 2$，求$\angle AFB$的余弦值.

答案：
(1) 证明：依题意，$\angle 1 = \angle 2$.
∵ 四边形 ABCD 是矩形，
∴ $AD // BC$.
∴ $\angle 2 = \angle 3$.
∴ $\angle 1 = \angle 3$.
∴ $BF = DF$,
∴ $\triangle BFD$ 为等腰三角形。
(2) 解：由
(1)可知 $BF = DF$. 设 $BF = x$, 则 $AF = 4 - x$, 在 Rt$\triangle BAF$ 中，$(4 - x)^2 + 2^2 = x^2$, 解得 $x = \frac{5}{2}$.
∴ $AF = 4 - \frac{5}{2} = \frac{3}{2}$.
∴ $\cos \angle AFB = \frac{AF}{BF} = \frac{3}{5}$.