《2025年作业本江西教育出版社九年级数学全一册北师大版》

1.方程$5(x^{2}-\sqrt{2}x + 1)= -3\sqrt{2}x + 2$的一般形式是$5x^{2}-2\sqrt{2}x+3=0$，其二次项是$5x^{2}$，一次项是$-2\sqrt{2}x$，常数项是3.

答案： $5x^{2}-2\sqrt{2}x+3=0$
$5x^{2}$
$-2\sqrt{2}x$
3

2.下列方程中，是一元二次方程的是①④(填序号).
①$x^{2}-2x - 1 = 0$；②$ax^{2}+bx + c = 0$；
③$\frac{1}{x^{2}}+3x - 5 = 0$；④$-x^{2}=0$；⑤$(x - 1)^{2}+y^{2}=2$；⑥$(x - 1)(x - 3)=x^{2}$.

答案： ①④

3.某班同学毕业时都向全班其他同学各送一张自己的照片留念，全班共送出$1190$张照片.若全班有$x$名同学，则可列方程为x(x-1)=1190.

答案： x(x-1)=1190

4.如果关于$x$的一元二次方程$ax^{2}+bx - 1 = 0$的一个解是$x = 1$，那么$2025 - a - b =$2024.

答案： 2024

5.若关于$x$的一元二次方程$(m - 2)x^{2}+2x + m^{2}-4 = 0$的常数项为$0$，求$m$的值.

答案：
∵关于$x$的一元二次方程$(m-2)x^{2}+2x+m^{2}-4=0$的常数项为$0$，
∴$m-2≠0$，$m^{2}-4=0$. 解得$m=-2$.

6.某超市销售一种品牌童装，平均每天可售出$30$件，每件盈利$40$元.为加快资金周转，超市采取降价措施，每件童装每降$2$元，平均每天可多售出$6$件.要使平均每天的销售利润为$1000$元，
那么每件童装应降价多少元？（列出方程并化为一般形式，不解答）

答案： 解：设每件童装降价$x$元.
根据题意，得$(30+3x)(40-x)=1000$，
整理，得$3x^{2}-90x-200=0$.

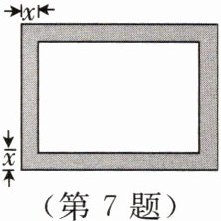
7.为改善校园环境，学校计划在一块长$80\ m$、宽$60\ m$的长方形场地中央建一个长方形网球场，网球场的占地面积为$3500\ m^{2}$，四周为宽度相等的人行道，如图所示，设人行道的宽为$x\ m$.
(1)请列出相应的方程.
(2)$x$可能小于$0$吗？$x$可能大于$40$吗？$x$可能大于$30$吗？请说明理由.
(3)你知道人行道的宽是多少吗？（直接写出结果即可）

答案： 1. （1）
已知长方形场地长$80m$、宽$60m$，人行道宽为$x m$，则网球场的长为$(80 - 2x)m$，宽为$(60 - 2x)m$。
根据长方形面积公式$S = 长×宽$，且网球场占地面积为$3500m^{2}$，可列方程：$(80 - 2x)(60 - 2x)=3500$。
2. （2）
$x$不可能小于$0$，因为$x$表示人行道的宽度，宽度不能为负数。
$x$不可能大于$40$，若$x\gt40$，则$80 - 2x\lt80-2×40 = 0$，而网球场的长不能为负数。
$x$不可能大于$30$，若$x\gt30$，则$60 - 2x\lt60 - 2×30=0$，而网球场的宽不能为负数。
3. （3）
先将方程$(80 - 2x)(60 - 2x)=3500$展开：
$4800-160x - 120x+4x^{2}=3500$。
整理得$4x^{2}-280x + 4800 - 3500 = 0$，即$4x^{2}-280x+1300 = 0$，两边同时除以$4$得$x^{2}-70x + 325 = 0$。
对于一元二次方程$ax^{2}+bx + c = 0(a = 1,b=-70,c = 325)$，根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$，其中$\Delta=b^{2}-4ac=(-70)^{2}-4×1×325=4900 - 1300 = 3600$。
则$x=\frac{70\pm\sqrt{3600}}{2}=\frac{70\pm60}{2}$。
$x_{1}=\frac{70 + 60}{2}=65$（舍去，因为$x = 65$时，$80-2x=80 - 130=-50\lt0$，$60 - 2x=60-130=-70\lt0$），$x_{2}=\frac{70 - 60}{2}=5$。
所以（1）方程为$(80 - 2x)(60 - 2x)=3500$；（2）$x$不可能小于$0$，不可能大于$40$，不可能大于$30$；（3）$x = 5$。