第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
1.如图所示,用两个转盘(其中一个转盘被分成两等份,另一个转盘被分成三等份)进行“配紫色”游戏:分别转动两个转盘,若其中一个转盘转出了红色,另一个转盘转出了蓝色,则可配成紫色.此时,配成紫色的概率是
]

$\frac{1}{3}$
,出现相同颜色的概率是$\frac{1}{3}$
.]

答案:
$\frac{1}{3}$
$\frac{1}{3}$
$\frac{1}{3}$
2.有两把不同的锁和四把不同的钥匙,其中只有两把钥匙恰好分别能打开这两把锁.现在任意取出一把钥匙去开任意一把锁.
(1)请用画树状图或列表的方法表示出上述试验所有可能的结果.
(2)求一次打开锁的概率.
(1)请用画树状图或列表的方法表示出上述试验所有可能的结果.
(2)求一次打开锁的概率.
答案:
解:
(1)设两把不同的锁分别为 A,B,能把两把锁打开的钥匙分别为 a,b,其余两把钥匙分别为 m,n,根据题意,可以画出如下树状图:
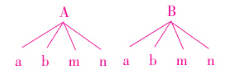
上述试验共有 8 种等可能的结果.
(2)$P$(一次打开锁)=$\frac{2}{8}$=$\frac{1}{4}$.
解:
(1)设两把不同的锁分别为 A,B,能把两把锁打开的钥匙分别为 a,b,其余两把钥匙分别为 m,n,根据题意,可以画出如下树状图:

上述试验共有 8 种等可能的结果.
(2)$P$(一次打开锁)=$\frac{2}{8}$=$\frac{1}{4}$.
3.某商场在元旦当天举行有奖促销活动,顾客一次性购物满 200 元可从以下两种奖励方案中任选其一:
方案一:直接获得 20 元礼金券.
方案二:参与一次转盘抽奖活动.规则
如下:如图所示,两个相同的可以自由转动的转盘 A 和 B,它们除颜色外无其他差别.抽奖时同时转动两个转盘,若指针停在分割线上,则需重新转动转盘.根据指针指向的区域颜色组合,可获得相应金额的礼金券,如下表所示.

(1)请用列表法或画树状图法求两个转盘指针分别指向一红区和一蓝区的概率.
(2)某顾客当天在该商场购物满 200 元,若只考虑获得最多的礼金券,请你分析选择哪种方案较为实惠.

方案一:直接获得 20 元礼金券.
方案二:参与一次转盘抽奖活动.规则
如下:如图所示,两个相同的可以自由转动的转盘 A 和 B,它们除颜色外无其他差别.抽奖时同时转动两个转盘,若指针停在分割线上,则需重新转动转盘.根据指针指向的区域颜色组合,可获得相应金额的礼金券,如下表所示.

(1)请用列表法或画树状图法求两个转盘指针分别指向一红区和一蓝区的概率.
(2)某顾客当天在该商场购物满 200 元,若只考虑获得最多的礼金券,请你分析选择哪种方案较为实惠.

答案:
解:
(1)画树状图如下
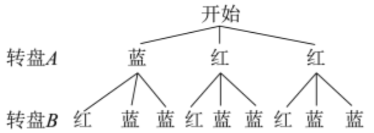
共有 9 种等可能的结果,其中转盘指针分别指向一红区和一蓝区的结果有 5 种,
∴两个转盘指针分别指向一红区和一蓝区的概率为$\frac{5}{9}$.
(2)
∵$P$(两红)=$P$(两蓝)=$\frac{2}{9}$,
∴如果选择方案二,那么获得礼金券的平均值为$\frac{5}{9}$×9+$\frac{2}{9}$×27+$\frac{2}{9}$×27=17(元).
∵17<20,
∴选择方案一比较实惠.
解:
(1)画树状图如下

共有 9 种等可能的结果,其中转盘指针分别指向一红区和一蓝区的结果有 5 种,
∴两个转盘指针分别指向一红区和一蓝区的概率为$\frac{5}{9}$.
(2)
∵$P$(两红)=$P$(两蓝)=$\frac{2}{9}$,
∴如果选择方案二,那么获得礼金券的平均值为$\frac{5}{9}$×9+$\frac{2}{9}$×27+$\frac{2}{9}$×27=17(元).
∵17<20,
∴选择方案一比较实惠.
查看更多完整答案,请扫码查看


