《2025年作业本江西教育出版社九年级数学全一册北师大版》

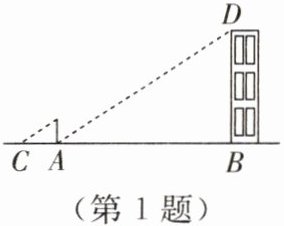
1. 如图所示，小明在测量楼高时，先测出楼房落在地面上的影长$BA$为$15\ m$，然后在$A$处竖立一根高$2\ m$的标杆，测得标杆的影长$AC$为$3\ m$，则楼高$BD$为10$m$.

答案： 10

2. 如图(示意图)所示，小东用长为$3.2\ m$的竹竿做测量工具测量学校旗杆的高度.移动竹竿，使竹竿和旗杆顶端的影子恰好落在地面上的同一点，此时，竹竿底端与这一点相距$8\ m$，与旗杆底端相距$22\ m$，则旗杆的高为12$m$.

答案： 12

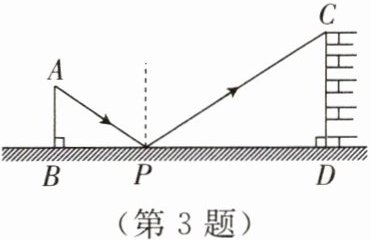
3. 小明设计用手电来测量古城墙高度的示意图如图所示.点$P$处放一水平的平面镜，光线从点$A$出发经平面镜反射后刚好射到古城墙$CD$的顶端$C$处.已知$AB\perp BD$，$CD\perp BD$，若测得$AB=1.2\ m$，$BP=1.8\ m$，$PD=12\ m$，则该古城墙的高度是8$m$.

答案： 8

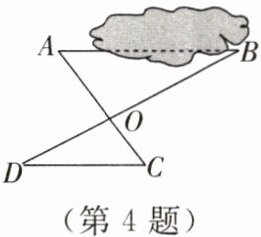
4. 为测量池塘边两点$A$，$B$之间的距离，小明设计了如下方案：在地面取一点$O$，使$AC$，$BD$交于点$O$，且$CD// AB$.若测得$OB:OD=3:2$，$CD=40\ m$，则$A$，$B$两点之间的距离为60$m$.

答案： 60

5. 如图所示，零件的外径为$16\ cm$，需求它的壁厚$x$，要先求出内径$AB$.现用一个交叉钳($AD$与$BC$相等)去量，测得$OA:OD=OB:OC=3:1$，$CD=5\ cm$，求出零件的壁厚$x$.

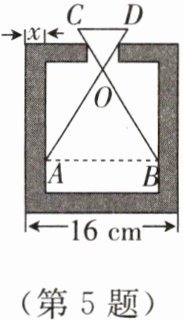
答案： 解：
∵$OA:OD=OB:OC=3:1$，$\angle COD=\angle AOB$，
∴$\triangle COD \sim \triangle BOA$.
∴$AB:CD=OA:OD=3:1$.
∵$CD=5\ cm$，
∴$AB=15\ cm$，
∴$2x+15=16$，
∴$x=0.5\ cm$.

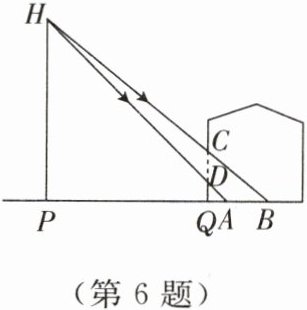
6. 如图所示，小超想要测量窗外的路灯$PH$的高度.某天晚上，他发现灯光透过窗户照射在房间的地板上，经过窗户的最高点$C$的灯光落在地板$B$处，经过窗户的最低点$D$的灯光落在地板$A$处，小超测得窗户距地面的高$QD=1\ m$，窗高$CD=1.5\ m$，并测得$AQ=1\ m$，$AB=2\ m$.请根据以上测量数据，求窗外的路灯的高度.

答案： 解：
∵$DQ\perp BP$，
∴$\angle CQB=90°$.
∵$QD=1\ m$，$QA=1\ m$，
∴$\angle QAD=45°$.
∵$PH\perp PB$，$\angle HAP=45°$，
∴$PH=PA$.
设$PH=PA=x\ m$.
∵$PH\perp PB$，$CQ\perp PB$，
∴$PH// CQ$，
∴$\triangle QBC \sim \triangle PBH$，
∴$\frac{CQ}{PH}=\frac{BQ}{PB}$，
∴$\frac{1.5+1}{x}=\frac{1+2}{x+2}$，解得$x=10$. 经检验，$x=10$是原方程的解且符合题意.