《2025年作业本江西教育出版社九年级数学全一册北师大版》

1. 学校新开设了航模、彩绘、泥塑三个社团，如果征征、舟舟两名同学每人随机选择参加其中一个社团，那么征征和舟舟选到同一个社团的概率为$\frac{1}{3}$.

答案： $\frac{1}{3}$

2. 从长度分别为2,4,6,7的四条线段中随机抽取三条，能构成三角形的概率是$\frac{1}{2}$.

答案： $\frac{1}{2}$

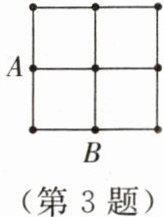
3. 如图所示，在$2 × 2$的正方形网格中有9个格点，已经取定点A和B，在余下的7个点中任取一点C，使$\bigtriangleup ABC$为直角三角形的概率是$\frac{4}{7}$.

答案： $\frac{4}{7}$

4. 某篮球运动员去年共参加40场比赛，其中三分球的命中率为0.25，平均每场有12个三分球未投中.
(1)该运动员在去年的比赛中共投中多少个三分球？
(2)在其中的一场比赛中，该运动员三分球共出手20次，小亮认为该运动员在这场比赛中一定投中了5个三分球.小亮的说法正确吗？

答案： 解：
(1)设该运动员共出手$x$个三分球.
根据题意，得$\frac{0.75x}{40}=12$，解得$x=640$.
$0.25x=0.25×640=160$(个).
(2)小亮的说法不正确.三分球的命中率为0.25，是相对于40场比赛来说的，而在其中的一场比赛中，虽然该运动员三分球共出手20次，但是该运动员本场比赛中不一定投中了5个三分球.

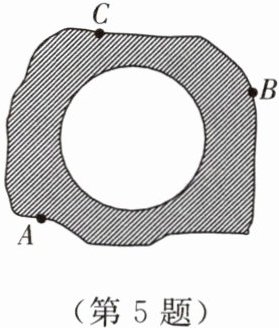
5. 小明在操场上做游戏，他发现地上有一个不规则的封闭图形$ABC$，为了知道它的面积，他在封闭图形内画了一个半径为1m的圆(如图所示)，在不远处向图形内掷石子，且记录如下：

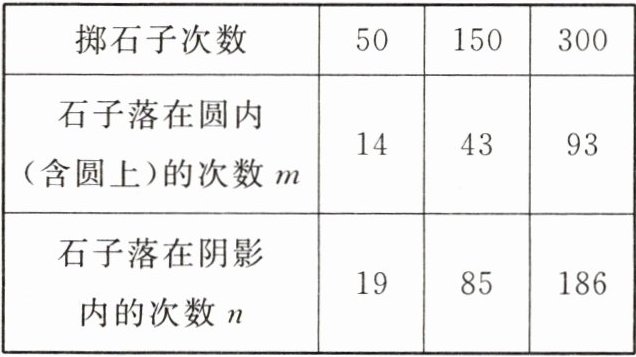
(1)随着次数的增多，小明发现$m$与$n$的比值在一个常数$k$附近波动，请你写出$k$的值.
(2)请利用学过的知识求出封闭图形$ABC$的大致面积.

答案： 解：
(1)根据统计表，可得石子落在圆内的次数与落在阴影内的次数之比$k=\frac{93}{186}=\frac{1}{2}$.
(2)随着试验次数的增多，石子落在圆内和阴影内的次数之比逐渐趋向于$1:2$，所以圆的面积约占封闭图形$ABC$面积的$\frac{1}{3}$.因为$S_{圆}=\pi\ \mathrm{m}^{2}$，所以封闭图形$ABC$的面积约为$3\pi\ \mathrm{m}^{2}$.