《2025年作业本江西教育出版社九年级数学全一册北师大版》

7. 在一个不透明的盒子中放入四张卡片，卡片上分别写有数字－2，－1，0，1，每张卡片除数字不同外，其他都相同. 从中随机抽取两张卡片，其数字之和为非负数的概率是$\frac{1}{3}$.

答案： $\frac{1}{3}$

8. 某同学手中有6张扑克牌，数字分别为1,2,3,4,5,6. 从中随机抽取2张，其牌面数字均为偶数的概率是$\frac{1}{5}$.

答案： $\frac{1}{5}$

9. 某班准备从甲、乙两名男生和丙、丁两名女生中任选两人分别任命为正、副值日班长.
(1) 求女生当选正值日班长的概率.
(2) 用列表或画树状图的方法求两名女生同时当选正、副值日班长的概率.

答案：
(1) 女生当选正值日班长的概率为 $\frac{2}{4}=\frac{1}{2}$。
(2) 列表如下：

副班长	正班长
甲	—	(乙,甲)	(丙,甲)	(丁,甲)
乙	(甲,乙)	—	(丙,乙)	(丁,乙)
丙	(甲,丙)	(乙,丙)	—	(丁,丙)
丁	(甲,丁)	(乙,丁)	(丙,丁)	—

共有12种等可能的情况，其中两名女生同时当选正、副值日班长的情况有2种，所以两名女生同时当选正、副值日班长的概率为 $\frac{2}{12}=\frac{1}{6}$。

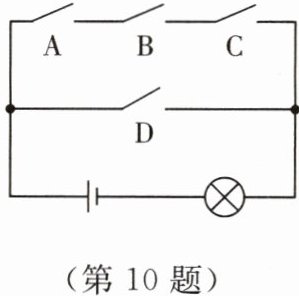
10. 如图所示，电路图中有A,B,C,D四个开关和一个小灯泡，闭合开关D或同时闭合开关A,B,C都可使小灯泡发光.
(1) 任意闭合一个开关，则小灯泡发光的概率为$\frac{1}{4}$.
(2) 任意闭合其中两个开关，用列表或画树状图的方法求小灯泡发光的概率.

答案：

(1) $\frac{1}{4}$
(2) 解：如图所示。

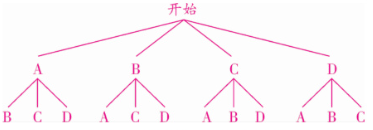
共有12种等可能的结果，其中能使小灯泡发光的结果有6种，
所以，小灯泡发光的概率是 $\frac{6}{12}=\frac{1}{2}$。