《2025年阳光学业评价八年级物理上册人教版》

1. 小明骑自行车在平直的公路上做匀速直线运动,以5 m/s的速度运动30 s,通过的距离是150m；以此速度运动300 m,所用时间是60s。

答案： 【解析】：
本题主要考查匀速直线运动的基本公式应用，即速度、路程和时间之间的关系。对于匀速直线运动，速度$v$、路程$s$和时间$t$之间满足关系式$v = \frac{s}{t}$。通过这个公式，我们可以求解出路程和时间。
对于第一个问题，已知速度和时间，我们可以直接通过公式$s = vt$计算出路程。
对于第二个问题，已知速度和路程，我们可以通过公式$t = \frac{s}{v}$计算出时间。
【答案】：
步骤一：计算通过的距离
已知速度$v = 5 m/s$，时间$t = 30 s$，
根据公式$s = vt$，有
$s = 5 × 30 = 150 m$
所以，通过的距离是$150 m$。
步骤二：计算运动$300 m$所用的时间
已知速度$v = 5 m/s$，路程$s = 300 m$，
根据公式$t = \frac{s}{v}$，有
$t = \frac{300}{5} = 60 s$
所以，运动$300 m$所用的时间是$60 s$。

2. 汽车甲的速度为30 m/s,汽车乙的速度为72 km/h,则两车中汽车甲(选填“汽车甲”或“汽车乙”)的速度较大。

答案： 解：汽车乙的速度为 $ v_{乙} = 72 \, km/h = 72 × \frac{1000 \, m}{3600 \, s} = 20 \, m/s $。
汽车甲的速度 $ v_{甲} = 30 \, m/s $，因为 $ 30 \, m/s ＞ 20 \, m/s $，所以汽车甲的速度较大。
汽车甲

3. 在高速公路上行驶的小轿车经过如图1-3-7甲所示的高架桥时,其速度表如图1-3-7乙所示。

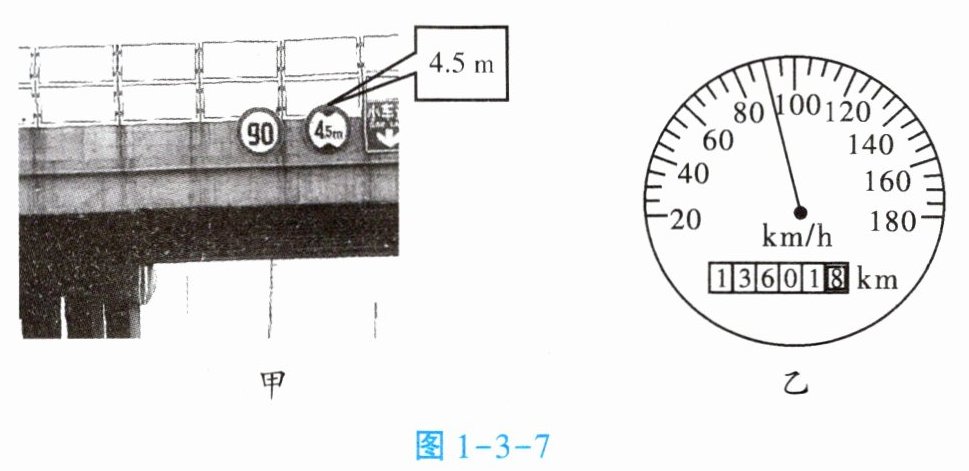
(1)请写出桥上两个标示牌中的数字所表示的意思。
“90”：此路段限速90km/h。“4.5 m”：此桥限高4.5m。
(2)小轿车的速度表显示它没有(选填“有”或“没有”)超速,小轿车此时的速度是80km/h。以此速度行驶0.5 h通过的路程为40km。

答案： 【解析】：
本题主要考察对速度限制牌和速度表的理解，以及速度、时间和路程之间的关系。
（1）首先，需要理解桥上的两个标示牌。
"90"通常表示速度限制，单位是$km/h$，意味着车辆在此路段行驶时，速度不得超过$90km/h$。
"4.5m"则通常表示此处桥梁的高度限制，单位是米，意味着超过此高度的车辆不得通过。
接下来，通过观察小轿车的速度表来解答第二问。
需要确定小轿车的当前速度，然后与速度限制进行比较，以判断是否超速。
最后，利用速度，时间，路程的基本关系公式 $s = vt$ 来计算小轿车以此速度行驶0.5h所通过的路程。
【答案】：
(1)"$90$"表示此路段限速$90km/h$；"$4.5m$"表示此桥限高$4.5m$。
(2)观察速度表可知，小轿车的速度$v = 80km/h$。
因为$ 80km/h ＜ 90km/h $，所以小轿车没有超速。
利用公式 $s = vt$，其中 $v = 80km/h$，$t = 0.5h$，
代入公式得：$s = 80 × 0.5 = 40km$。
故答案为：没有；$80$；$40km$。