《2025年新课程课堂同步练习册五年级数学上册苏教版》

1. 小数的末尾(添上)“0”或(去掉)“0”,小数的(大小)不变。这是小数的(性质)。

答案： 解析：本题考查小数的基本性质。小数的末尾添上“0”或去掉“0”，小数的大小不变，这是小数的性质。
答案：添上，去掉，大小，性质。

2. 1.5和1.50的大小(相等),计数单位(不同)。

答案： 解析：本题考查小数的大小比较以及小数的计数单位。
首先，我们来看1.5和1.50的大小关系。
根据小数的性质，我们知道在小数的末尾添上“0”或者去掉”0“，小数的大小不变。
因此，1.5和1.50表示的是同一个数，即它们的大小相等。
接下来，我们来看1.5和1.50的计数单位。
一位小数的计数单位是0.1，两位小数的计数单位是0.01。
1.5是一位小数，所以它的计数单位是0.1；
而1.50是两位小数，所以它的计数单位是0.01。
答案：相等；不同。

3. 把整数改写成小数时,不要忘记在整数个位右下角点上小数点。

答案： 解析：本题考查整数改写成小数的方法。
把整数改写成小数时，要在整数个位右下角点上小数点，然后根据需要在小数部分添上相应数量的0。
答案：小数点。

4. 把100改写成两位小数是(100.00),改写成一位小数是(100.0)。

答案： 解析：本题考查小数的性质，即小数的末尾添上“0”或去掉“0”，小数的大小不变。利用这一性质，可以把一个整数或小数改写成指定小数位数的小数。
答案：100.00；100.0

5. 把7改写成以百分之一作计数单位的数是(7.00)。

答案： 解析：本题考查小数的性质以及计数单位的知识点。以百分之一作计数单位，即要将数字改写成两位小数。对于整数7，可以写成7.00，这样它就以百分之一（0.01）作计数单位了。
答案：7.00。

6. 一个不安分的小数点,从原来的位置向左跳动2位,又向右跳动3位,这时所得的数是83。原来的数是(8.3)。

答案： 解析：题目考查小数的性质及小数点位置的移动与小数大小的变化规律。
设原数为$x$，小数点向左跳动$2$位，相当于原数除以$100$，即$\frac{x}{100}$；接着又向右跳动$3$位，相当于再乘以$1000$，则变为$\frac{x}{100}×1000 = 10x$。
已知这时所得的数是$83$，即$10x = 83$，那么原数$x = 83÷10 = 8.3$。
答案：$8.3$。

二、化简下面的小数。
4.60 = 4.6
0.300 = 0.3
5.080 = 5.08
60.0300 = 60.03

答案： 解析：本题主要考查小数的性质，即小数的末尾添上“0”或去掉“0”，小数的大小不变。根据这一性质，我们可以直接去掉各小数末尾的0来化简小数。
答案：
4.60 = 4.6
0.300 = 0.3
5.080 = 5.08
60.0300 = 60.03

三、把下面各数改写成三位小数。
3.5 = 3.500
20.00 = 20.000
12.8 = 12.800
15.5250 = 15.525

答案： 解析：本题考查的是小数的性质，即在小数的末尾添上“0”或者去掉”0“，小数的大小不变。我们要将给定的数改写成三位小数，只需在小数末尾补足0即可。
答案：
3.5 = 3.500，
20.00 = 20.000，
12.8 = 12.800，
15.5250 = 15.525。

四、把下面的钱数改写成用“元”作单位的两位小数。
8角5分是(0.85)元 10元2角是(10.20)元 5角是(0.50)元

答案： 解析：本题考查的是小数的性质以及元、角、分之间的换算。
根据1元 = 10角，1角 = 10分，1元 = 100分，可得：
8角5分可以换算成元是：8角是 0.8 元，5分是 0.05 元，所以 8 角 5 分是 0.85 元。
10元2角可以换算成元是：10元就是 10 元，2角是 0.2 元，所以 10 元 2 角是 10.20 元。
5角可以换算成元是：5角是 0.5 元，换算成两位小数就是 0.50 元。
答案：0.85；10.20；0.50。

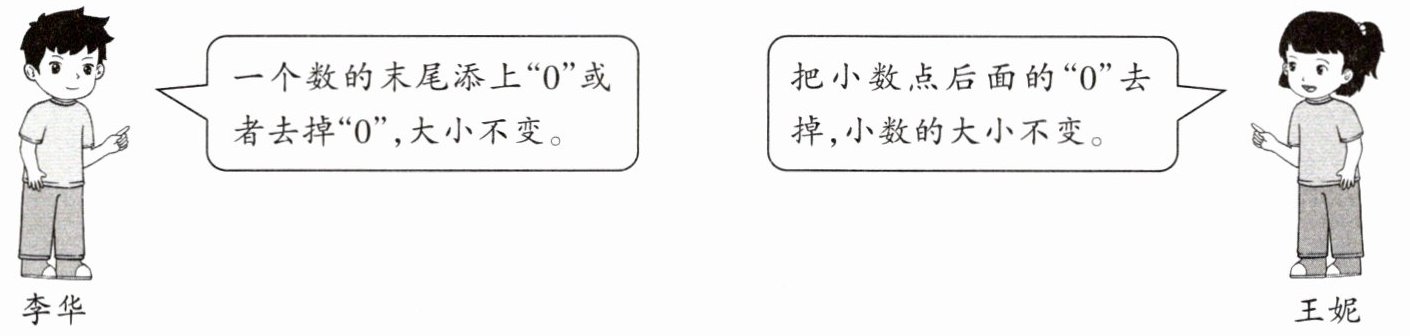
五、下面两位同学的说法正确吗？为什么？可举例说明。

答案： 李华的说法错误，王妮的说法也错误。
李华：只有在小数的末尾添上“0”或者去掉“0”，小数的大小才不变。例如$2.3$，在末尾添上一个$0$变为$2.30$，$2.3 = 2.30$；但如果是在$203$这样的整数末尾添$0$，$203$变为$2030$，数值大小改变了，所以李华说法错误。
王妮：把小数点后面的“0”去掉，小数的大小可能会改变。例如$2.03$，去掉小数点后面的$0$变为$2.3$，$2.03\neq2.3$ ，只有在小数的末尾的$0$去掉才不改变大小，所以王妮说法错误。

六、找规律填数。
1. 3.2,4.2,5.2,(6.2),(7.2)。
2. 0.02,0.04,0.06,(0.08),(0.10)。

答案： 解析：这两道题都是找规律填数的问题，需要观察数列中数的变化规律，然后依据规律填写缺失的数。
1. 对于第一题，观察数列3.2，4.2，5.2，可以看出每个数都比前一个数多1，因此这是一个等差数列，公差为1。所以，接下来的两个数应该是5.2加1和5.2加2，即6.2和7.2。
2. 对于第二题，观察数列0.02，0.04，0.06，可以看出每个数都比前一个数多0.02，因此这也是一个等差数列，公差为0.02。所以，接下来的两个数应该是0.06加0.02和0.06加0.04，即0.08和0.10。
答案：
1. 3.2，4.2，5.2，(6.2)，(7.2)。
2. 0.02，0.04，0.06，(0.08)，(0.10)。

七、先做五张卡片,分别写上0、0、3、5和小数点,再按要求摆数。(所有的卡片都用上,每题写2个)
1. 所有的“0”都不能去掉：(0.035,0.053)。
2. 只能去掉1个“0”而大小不变的是(3.050,5.030)。

答案： 解析：本题考查小数的性质，特别是小数末尾的“0”对小数大小的影响。
1.对于所有的“0”都不能去掉的情况，需要构造出小数中的“0”不是都在末尾的，或者只有部分“0”在小数末尾但去掉后会改变小数的大小或变成整数。考虑到我们手头有数字0、0、3、5，可以构造出类似这样的数，其中一个“0”在小数点后但不是末尾，另一个“0”在更后面的位置或者整数部分。
答案：
(1). 所有的“0”都不能去掉：(0.035, 0.053)（答案不唯一）。
2.对于只能去掉1个“0”而大小不变的情况，需要构造出一个小数，其中只有一个“0”是在小数末尾的，而另一个“0”则不在末尾。这样，当我们去掉末尾的“0”时，小数的大小不会改变，但去掉非末尾的“0”则会改变。考虑到我们手头的数字，可以构造出类似3.050或5.030这样的数，其中只有一个“0”是多余的，可以去掉而不改变小数的大小。
答案：
(2). 只能去掉1个“0”而大小不变的是：(3.050, 5.030)（答案不唯一）。