《2025年初中同步测控优化设计九年级数学全一册人教版》

1. 下列图标中,是中心对称图形的是(B)

答案： B

2. 在平面直角坐标系中,线段 $ OP $ 的两个端点坐标分别为 $ O(0,0) $,$ P(4,3) $,将线段 $ OP $ 绕点 $ O $ 逆时针旋转 $ 90^{\circ} $ 到 $ OP' $ 位置,则点 $ P' $ 的坐标为(C)
A.$ (3,4) $
B.$ (-4,3) $
C.$ (-3,4) $
D.$ (4,-3) $

答案： C

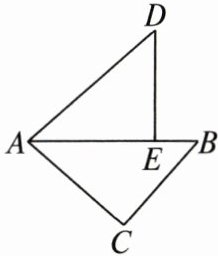
3. 如图,在 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ AC = 4 $,$ BC = 3 $,将 $ \triangle ABC $ 绕点 $ A $ 逆时针旋转,使点 $ C $ 落在线段 $ AB $ 上的点 $ E $ 处,点 $ B $ 落在点 $ D $ 处,则 $ B $,$ D $ 两点间的距离为(√10)

A.$ \sqrt{10} $
B.$ 2\sqrt{2} $
C.$ 3 $
D.$ 2\sqrt{5} $

答案： A 连接BD.由勾股定理,得AB=√(AC²+BC²)=√(4²+3²)=5,AE=AC=4,所以BE=1.又DE=3,∠DEA=∠C=90°,所以BD=√(DE²+BE²)=√(1+9)=√10.

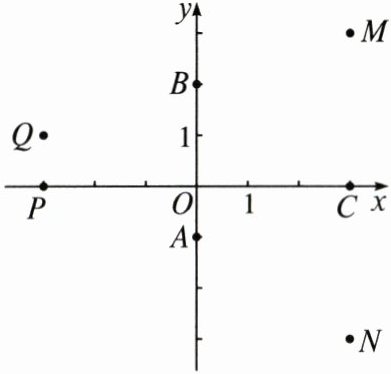
4. 如图,点 $ A $,$ B $,$ C $ 的坐标分别为 $ (0,-1) $,$ (0,2) $,$ (3,0) $。从下面四个点 $ M(3,3) $,$ N(3,-3) $,$ P(-3,0) $,$ Q(-3,1) $ 中选择一个点,以 $ A $,$ B $,$ C $ 及该点为顶点的四边形是中心对称图形的个数为(C)

A.$ 1 $
B.$ 2 $
C.$ 3 $
D.$ 4 $

答案： C

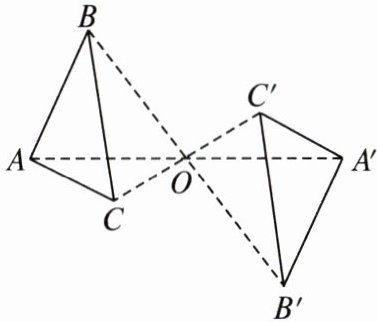
5. 如图,$ \triangle ABC $ 与 $ \triangle A'B'C' $ 关于点 $ O $ 成中心对称,则下列结论不正确的是(D)

A.$ S_{\triangle ABC} = S_{\triangle A'B'C'} $
B.$ AB = A'B' $,$ AC = A'C' $,$ BC = B'C' $
C.$ AB // A'B' $,$ AC // A'C' $,$ BC // B'C' $
D.$ S_{\triangle A'B'O} = S_{\triangle ACO} $

答案： D

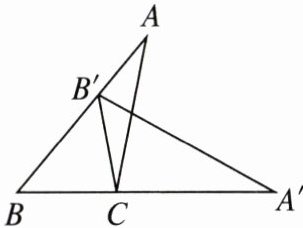
6. 如图,将 $ \triangle ABC $ 绕点 $ C $ 顺时针旋转,使点 $ B $ 落在 $ AB $ 边上点 $ B' $ 处,此时,点 $ A $ 的对应点 $ A' $ 恰好落在 $ BC $ 边的延长线上,下列结论错误的是(C)

A.$ \angle BCB' = \angle ACA' $
B.$ \angle ACB = 2\angle B $
C.$ \angle B'CA = \angle B'AC $
D.$ B'C $ 平分 $ \angle BB'A' $

答案： C

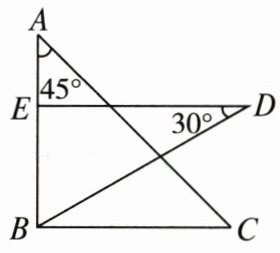
7. 把一副三角板按如图放置,其中 $ \angle ABC = \angle DEB = 90^{\circ} $,$ \angle A = 45^{\circ} $,$ \angle D = 30^{\circ} $,斜边 $ AC = BD = 10 $,若将三角板 $ DEB $ 绕点 $ B $ 逆时针旋转 $ 45^{\circ} $ 得到 $ \triangle D'E'B $,则点 $ A $ 在 $ \triangle D'E'B $ 的(C)

A.内部
B.外部
C.边上
D.以上都有可能

答案： C 由三角板DEB绕点B逆时针旋转45°得到△D'E'B,设△D'E'B与直线AB交于点M,可知∠EBE'=45°,∠E'=∠DEB=90°.
∵∠DEB=90°,∠D=30°,BD=10,
∴BE=5,
∴BE'=BE=5,
∴BM=5√2.又∠ABC=90°,∠A=45°,AC=10,
∴AB=5√2,
∴BM=AB,
∴点A在△D'E'B的D'E'的边上.