16. 为创建绿色校园,学校决定对一块正方形的空地进行种植花草,现向学生征集设计图案。图案要求只能用圆弧在正方形内加以设计,使正方形和所画的圆弧构成图案,种植花草部分用阴影表示。请你运用平移、旋转、轴对称等知识,在图③、图④、图⑤中画出三种不同的设计图案(温馨提示:在两个图案中,只有半径变化而圆心不变的图案属于同一种,例如:图①、图②只能算一种)。


答案:
解答案不唯一,如下各图供参考.
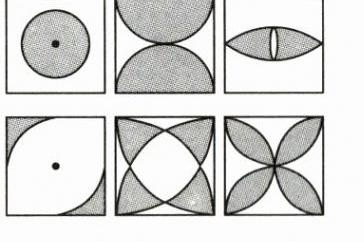
解答案不唯一,如下各图供参考.

17. 如图①,有一张矩形纸片,将它沿对角线 $ AC $ 剪开,得到 $ \triangle ACD $ 和 $ \triangle A'BC' $。
(1) 如图②,将 $ \triangle ACD $ 沿 $ A'C' $ 边向上平移,使点 $ A $ 与点 $ C' $ 重合,连接 $ A'D $ 和 $ BC $,则四边形 $ A'BCD $ 是
(2) 如图③,将 $ \triangle ACD $ 的顶点 $ A $ 与 $ A' $ 点重合,然后绕点 $ A $ 沿逆时针方向旋转,使点 $ D $,$ A $,$ B $ 在同一条直线上,则旋转角为
(3) 如图④,将 $ AC $ 边与 $ A'C' $ 边重合,并使顶点 $ B $ 和 $ D $ 在 $ AC $ 边的同一侧,设 $ AB $,$ CD $ 相交于 $ E $ 点,连接 $ BD $,四边形 $ ADBC $ 是什么特殊四边形?请说明你的理由。

(1) 如图②,将 $ \triangle ACD $ 沿 $ A'C' $ 边向上平移,使点 $ A $ 与点 $ C' $ 重合,连接 $ A'D $ 和 $ BC $,则四边形 $ A'BCD $ 是
平行四边
形;(2) 如图③,将 $ \triangle ACD $ 的顶点 $ A $ 与 $ A' $ 点重合,然后绕点 $ A $ 沿逆时针方向旋转,使点 $ D $,$ A $,$ B $ 在同一条直线上,则旋转角为
90
度,连接 $ CC' $,则四边形 $ CDBC' $ 是直角梯
形;(3) 如图④,将 $ AC $ 边与 $ A'C' $ 边重合,并使顶点 $ B $ 和 $ D $ 在 $ AC $ 边的同一侧,设 $ AB $,$ CD $ 相交于 $ E $ 点,连接 $ BD $,四边形 $ ADBC $ 是什么特殊四边形?请说明你的理由。

四边形ADBC是等腰梯形.理由如下:如图,过点B作BM⊥AC,过点D作DN⊥AC,垂足分别为M,N,因为有一张矩形纸片,将它沿对角线AC剪开,得到△ACD和△A'BC',所以△ACD≌△A'BC'.所以BM=ND.所以BD//AC.因为AD=BC,所以四边形ADBC是等腰梯形.
答案:
解
(1)因为AD=AB,AA'=AC,所以A'C与BD互相平分.所以四边形A'BCD是平行四边形.故答案为“平行四边”.
(2)因为DA垂直于AB,又知逆时针旋转到点D,A,B在同一直线上,所以旋转角为90度.因为∠D=∠B=90°,A,D,B在同一条直线上,所以CD//BC'.所以四边形CDBC'是直角梯形.故答案为“90 直角梯”.
(3)四边形ADBC是等腰梯形.理由如下:如图,过点B作BM⊥AC,过点D作DN⊥AC,垂足分别为M,N,因为有一张矩形纸片,将它沿对角线AC剪开,得到△ACD和△A'BC',所以△ACD≌△A'BC'.所以BM=ND.所以BD//AC.因为AD=BC,所以四边形ADBC是等腰梯形.
(1)因为AD=AB,AA'=AC,所以A'C与BD互相平分.所以四边形A'BCD是平行四边形.故答案为“平行四边”.
(2)因为DA垂直于AB,又知逆时针旋转到点D,A,B在同一直线上,所以旋转角为90度.因为∠D=∠B=90°,A,D,B在同一条直线上,所以CD//BC'.所以四边形CDBC'是直角梯形.故答案为“90 直角梯”.
(3)四边形ADBC是等腰梯形.理由如下:如图,过点B作BM⊥AC,过点D作DN⊥AC,垂足分别为M,N,因为有一张矩形纸片,将它沿对角线AC剪开,得到△ACD和△A'BC',所以△ACD≌△A'BC'.所以BM=ND.所以BD//AC.因为AD=BC,所以四边形ADBC是等腰梯形.
查看更多完整答案,请扫码查看


