1. 下列函数是关于 $ x $ 的二次函数的是(
A.$ y = ax^{2}+bx + c $
B.$ y = x^{2}+\frac{1}{x^{2}} $
C.$ y = (x + 1)^{2}-x^{2} $
D.$ y = x(1 - x) $
D
)A.$ y = ax^{2}+bx + c $
B.$ y = x^{2}+\frac{1}{x^{2}} $
C.$ y = (x + 1)^{2}-x^{2} $
D.$ y = x(1 - x) $
答案:
D
2. 若点 $ (2,5),(4,5) $ 在抛物线 $ y = ax^{2}+bx + c $ 上, 则它的对称轴是直线(
A.$ x = -\frac{b}{a} $
B.$ x = 1 $
C.$ x = 2 $
D.$ x = 3 $
D
)A.$ x = -\frac{b}{a} $
B.$ x = 1 $
C.$ x = 2 $
D.$ x = 3 $
答案:
D
3. 在平面直角坐标系中, 将抛物线 $ y = x^{2}-(m - 1)x + m(m>1) $ 沿 $ y $ 轴向下平移 $ 3 $ 个单位长度, 则平移后得到的抛物线的顶点一定在(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
D
4. 若抛物线 $ y = x^{2}+2x + m - 1 $ 与 $ x $ 轴有两个不同的交点, 则实数 $ m $ 的取值范围是(
A.$ m<2 $
B.$ m>2 $
C.$ 0<m\leqslant 2 $
D.$ m<-2 $
A
)A.$ m<2 $
B.$ m>2 $
C.$ 0<m\leqslant 2 $
D.$ m<-2 $
答案:
A
5. 一次函数 $ y = ax + c(a\neq 0) $ 与二次函数 $ y = ax^{2}+bx + c(a\neq 0) $ 在同一个坐标系中的图象可能是(

D
)
答案:
D 当x=0时,都有y=c,所以直线和抛物线都过点(0,c),排除A;对于B,由直线知a<0,由抛物线知a>0,矛盾;对于C,由直线知a>0,由抛物线知a<0,矛盾.只有D符合.
6. 关于 $ x $ 的二次函数 $ y = ax^{2}+bx + c $ 的图象如图所示, 若点 $ A(1,y_{1}),B(2,y_{2}) $ 是图象上的两点, 则 $ y_{1} $ 与 $ y_{2} $ 的大小关系是(
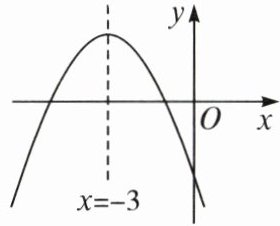
A.$ y_{1}<y_{2} $
B.$ y_{1}= y_{2} $
C.$ y_{1}>y_{2} $
D.不能确定
C
)
A.$ y_{1}<y_{2} $
B.$ y_{1}= y_{2} $
C.$ y_{1}>y_{2} $
D.不能确定
答案:
C 由图象可知对称轴的右侧y随x的增大而减小,随着x由1到2的增大,y值减小,即y₁>y₂.
7. 足球运动员将足球沿与地面成一定角度的方向踢出, 足球飞行的路线是一条抛物线, 不考虑空气阻力, 足球距离地面的高度 $ h $ (单位: $ m $) 与足球被踢出后经过的时间 $ t $ (单位: $ s $) 之间的关系如下表:

下列结论: ①足球距离地面的最大高度为 $ 20m $; ②足球飞行路线的对称轴是直线 $ t= \frac{9}{2} $; ③足球被踢出 $ 9s $ 时落地; ④足球被踢出 $ 1.5s $ 时, 距离地面的高度是 $ 11m $. 其中正确结论的个数是(
A.$ 1 $
B.$ 2 $
C.$ 3 $
D.$ 4 $

下列结论: ①足球距离地面的最大高度为 $ 20m $; ②足球飞行路线的对称轴是直线 $ t= \frac{9}{2} $; ③足球被踢出 $ 9s $ 时落地; ④足球被踢出 $ 1.5s $ 时, 距离地面的高度是 $ 11m $. 其中正确结论的个数是(
B
)A.$ 1 $
B.$ 2 $
C.$ 3 $
D.$ 4 $
答案:
B 由题意,设抛物线的解析式为h=at(t - 9),把(1,8)代入可得a = - 1,故h = - t² + 9t = - (t - 4.5)² + 20.25,所以足球距离地面的最大高度为20.25m,①错误.所以抛物线的对称轴为直线t = 4.5,②正确.当t = 9时,h = 0,即足球被踢出9s时落地,③正确.当t = 1.5时,h = 11.25,④错误.综上所述,正确的有②③.故选B.
查看更多完整答案,请扫码查看


