7. 如图,点 $ F $ 是 $ □ ABCD $ 的边 $ CD $ 上一点,直线 $ BF $ 交 $ AD $ 的延长线于点 $ E $,则下列结论错误的是(

A.$ \frac{ED}{EA} = \frac{DF}{AB} $
B.$ \frac{DE}{BC} = \frac{EF}{FB} $
C.$ \frac{BC}{DE} = \frac{BF}{BE} $
D.$ \frac{BF}{BE} = \frac{BC}{AE} $
C
)
A.$ \frac{ED}{EA} = \frac{DF}{AB} $
B.$ \frac{DE}{BC} = \frac{EF}{FB} $
C.$ \frac{BC}{DE} = \frac{BF}{BE} $
D.$ \frac{BF}{BE} = \frac{BC}{AE} $
答案:
C
8. 如图,小正方形的边长均为 $ 1 $,则下列图形中的三角形(阴影部分)与 $ \triangle ABC $ 相似的是(

B
)
答案:
B
9. 如图,已知图中的每个小方格都是边长为 $ 1 $ 的小正方形,每个小正方形的顶点称为格点. 若 $ \triangle ABC $ 与 $ \triangle A_1B_1C_1 $ 是位似图形,且顶点都在格点上,则位似中心的坐标是______.


答案:
(9,0) 要确定△ABC与△A₁B₁C₁的位似中心,只要连接A₁A,C₁C并延长,其交点即为位似中心,然后再根据画图的结果,确定位似中心的坐标即可.
10. $ \triangle ABC $ 的三边长分别为 $ 5 $,$ 12 $,$ 13 $,与它相似的 $ \triangle DEF $ 的最小边长为 $ 15 $,则 $ \triangle DEF $ 的周长为
90
.
答案:
90
∵△ABC的三边长分别为5,12,13,
∴△ABC的周长为5+12+13=30.
∵与它相似的△DEF的最小边长为15,
∴△DEF的周长:△ABC的周长=15:5=3:1,
∴△DEF的周长为3×30=90.
∵△ABC的三边长分别为5,12,13,
∴△ABC的周长为5+12+13=30.
∵与它相似的△DEF的最小边长为15,
∴△DEF的周长:△ABC的周长=15:5=3:1,
∴△DEF的周长为3×30=90.
11. 如图,$ AB $ 为 $ \odot O $ 的直径,$ C $ 为 $ \odot O $ 上一点,弦 $ AD $ 平分 $ \angle BAC $,交 $ BC $ 于点 $ E $,若 $ AB = 6 $,$ AD = 5 $,则 $ AE $ 的长为

$\frac{14}{5}$
.
答案:
$\frac{14}{5}$
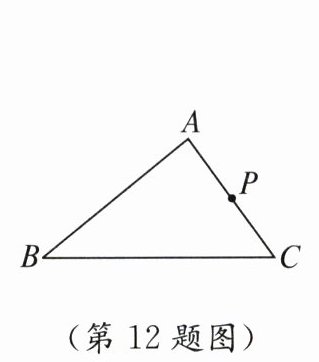
12. 如图,在 $ \triangle ABC $ 中,$ AB = 6 $,$ AC = 4 $,$ P $ 是 $ AC $ 的中点,过点 $ P $ 的直线交 $ AB $ 于点 $ Q $. 若以 $ A $,$ P $,$ Q $ 为顶点的三角形和以 $ A $,$ B $,$ C $ 为顶点的三角形相似,则 $ AQ $ 的长为
3或$\frac{4}{3}$
.
答案:
3或$\frac{4}{3}$ 由于以A,P,Q为顶点的三角形和以A,B,C为顶点的三角形有一个公共角(∠A),因此依据相似三角形的判定方法,过点P的直线PQ应有两种作法:一是过点P作PQ//BC,这样根据相似三角形的性质可得$\frac{AQ}{AB}=\frac{AP}{AC}$,即$\frac{AQ}{6}=\frac{2}{4}$,解得AQ=3;二是过点P作∠APQ=∠ABC,交边AB于点Q,这时△APQ∽△ABC,于是有$\frac{AQ}{AC}=\frac{AP}{AB}$,即$\frac{AQ}{4}=\frac{2}{6}$,解得$AQ=\frac{4}{3}$.综上,AQ的长为3或$\frac{4}{3}$.
13. 一古老的捣碎器如图所示,已知支撑柱 $ AB $ 的高为 $ 0.3 \, m $,踏板 $ DE $ 长为 $ 1.6 \, m $,支撑点 $ A $ 到踏脚 $ D $ 的距离为 $ 0.6 \, m $,现在踏脚着地,则捣头点 $ E $ 距地面______

0.8
$ m $.
答案:
0.8
∵△ABD∽△ECD,
∴AD:ED=AB:EC,
∴0.6:1.6=0.3:EC,解得EC=0.8m.
∵△ABD∽△ECD,
∴AD:ED=AB:EC,
∴0.6:1.6=0.3:EC,解得EC=0.8m.
查看更多完整答案,请扫码查看


