《2025年初中同步测控优化设计九年级数学全一册人教版》

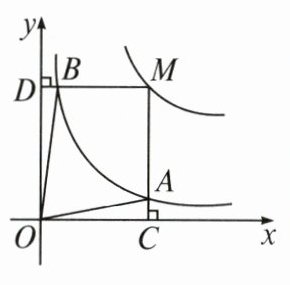
8. 反比例函数$y= \frac{a}{x}(a＞0$,$a为常数)和y= \frac{2}{x}$在第一象限内的图象如图所示。已知点$M在y= \frac{a}{x}$的图象上,$MC\perp x轴于点C$,交$y= \frac{2}{x}的图象于点A$。$MD\perp y轴于点D$,交$y= \frac{2}{x}的图象于点B$,则当点$M在y= \frac{a}{x}$的图象上运动时,以下结论：
①$S_{\triangle ODB}= S_{\triangle OCA}$；
②四边形$OAMB$的面积不变；
③当点$A是MC$的中点时,则点$B是MD$的中点。
其中正确结论的个数是( )


A.$0$
B.$1$
C.$2$
D.$3$

答案：
D ①$S_{\triangle ODB}=S_{\triangle OCA}=1$，该结论正确。②四边形$OAMB$的面积$=a - 1 - 1 = a - 2$，面积不变，该结论正确。③如图，连接$OM$，点$A$是$MC$的中点，则$\triangle OAM$和$\triangle OAC$的面积相等。因为$\triangle ODM$的面积等于$\triangle OCM$的面积，$\triangle ODB$的面积等于$\triangle OCA$的面积，所以$\triangle OAC$，$\triangle OAM$，$\triangle OBD$，$\triangle OBM$面积相等，均为矩形$OCMD$面积的四分之一，由$\triangle OBD$和$\triangle OBM$面积相等，且高$OD$相同，可知底$BD$与$BM$相等，所以点$B$是$MD$的中点，该结论正确。

9. 已知反比例函数$y= \frac{k}{x}的图象经过点(1,-8)$,则$k= $-8。

答案： -8

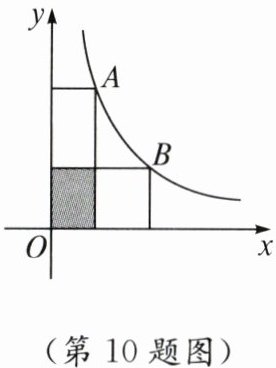
10. 如图,点$A$,$B是双曲线y= \frac{6}{x}$上的点,分别过点$A$,$B作x轴和y$轴的垂线段,若图中阴影部分的面积为$2$,则两个空白矩形面积的和为______。

答案：
8 如图，
∵点$A$，$B$是双曲线$y=\frac{6}{x}$上的点，
∴$S_{矩形ACOG}=S_{矩形BEOF}=6$。
∵$S_{阴影DOGF}=2$，
∴$S_{矩形ACFD}+S_{矩形BEGC}=6 + 6 - 2 - 2 = 8$。

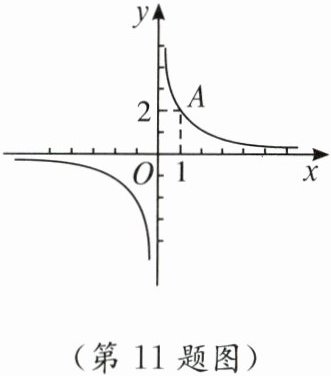
11. 如图,反比例函数$y= \frac{k}{x}$的图象位于第一、三象限,其中第一象限内的图象经过点$A(1,2)$,请在第三象限内的图象上找一个你喜欢的点$P$,你选择的点$P$的坐标为$(-1,-2)$。

答案： 答案不唯一，如$(-1,-2)$ $x$，$y$满足$xy = 2$，且$x＜0$，$y＜0$即可。

12. 过反比例函数$y= \frac{k}{x}(k\neq0)图象上的一点A$,分别作$x$轴、$y$轴的垂线,垂足分别为点$B$,$C$,若$\triangle ABC的面积为3$,则$k$的值为6或$-6$。

答案： 6或$-6$ 根据反比例函数的几何意义可得出$S_{\triangle ABC}=\frac{1}{2}|k|$，所以$|k| = 6$，则$k = ±6$。

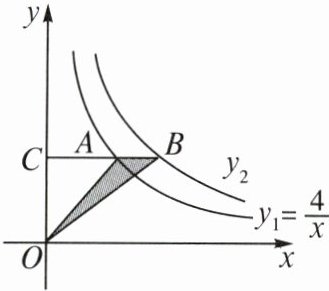
13. 双曲线$y_{1}$,$y_{2}$在第一象限的图象如图所示,$y_{1}= \frac{4}{x}$,过$y_{1}上的任意一点A作x轴的平行线交$y_{2}$于点B$,交$y轴于点C$,若$S_{\triangle AOB}= 1$,则$y_{2}$的解析式是$y_{2}=\frac{6}{x}$。

答案： $y_{2}=\frac{6}{x}$ 因为点$A$在双曲线$y_{1}$上，所以$S_{\triangle AOC}=2$。又$S_{\triangle AOB}=1$，所以$\triangle CBO$的面积为$3$。所以$y_{2}$的解析式是$y_{2}=\frac{6}{x}$。