1. 如图,直线 $ l_1 // l_2 // l_3 $,直线 $ AC $ 分别交 $ l_1 $,$ l_2 $,$ l_3 $ 于点 $ A $,$ B $,$ C $,直线 $ DF $ 分别交 $ l_1 $,$ l_2 $,$ l_3 $ 于点 $ D $,$ E $,$ F $,$ AC $ 与 $ DF $ 相交于点 $ H $,且 $ AH = 2 $,$ HB = 1 $,$ BC = 5 $,则 $ \frac{DE}{EF} $ 的值为(

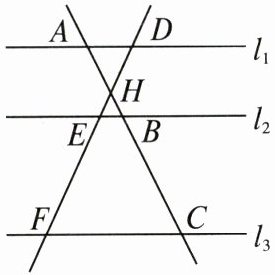
A.$ \frac{1}{2} $
B.$ 2 $
C.$ \frac{2}{5} $
D.$ \frac{3}{5} $
D
)

A.$ \frac{1}{2} $
B.$ 2 $
C.$ \frac{2}{5} $
D.$ \frac{3}{5} $
答案:
D
2. 如图,锐角三角形 $ ABC $ 的高 $ CD $ 和高 $ BE $ 相交于点 $ O $,则与 $ \triangle DOB $ 相似的三角形个数是(
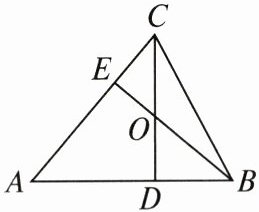
A.$ 1 $
B.$ 2 $
C.$ 3 $
D.$ 4 $
C
)
A.$ 1 $
B.$ 2 $
C.$ 3 $
D.$ 4 $
答案:
C
3. 如图,在平面直角坐标系中,矩形 $ OABC $ 的顶点 $ O $ 在坐标原点,边 $ OA $ 在 $ x $ 轴上,$ OC $ 在 $ y $ 轴上. 如果矩形 $ OA'B'C' $ 与矩形 $ OABC $ 关于点 $ O $ 位似,且矩形 $ OA'B'C' $ 的面积等于矩形 $ OABC $ 面积的 $ \frac{1}{4} $,那么点 $ B' $ 的坐标是(
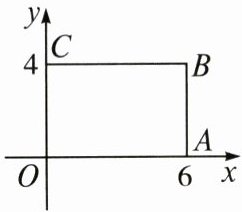
A.$ (3,2) $
B.$ (-2,-3) $
C.$ (2,3) $ 或 $ (-2,-3) $
D.$ (3,2) $ 或 $ (-3,-2) $
D
)
A.$ (3,2) $
B.$ (-2,-3) $
C.$ (2,3) $ 或 $ (-2,-3) $
D.$ (3,2) $ 或 $ (-3,-2) $
答案:
D
4. 如图,在 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ D $ 是 $ AC $ 上一点,$ DE \perp AB $ 于点 $ E $. 若 $ AC = 8 $,$ BC = 6 $,$ DE = 3 $,则 $ AD $ 的长为(
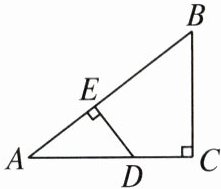
A.$ 3 $
B.$ 4 $
C.$ 5 $
D.$ 6 $
C
)
A.$ 3 $
B.$ 4 $
C.$ 5 $
D.$ 6 $
答案:
C
5. 已知 $ \triangle ABC $ 三个顶点的坐标分别为 $ (1,2) $,$ (-2,3) $,$ (-1,0) $,把它们的横坐标和纵坐标分别变成原来的 $ 2 $ 倍,得到点 $ A' $,$ B' $,$ C' $. 下列说法正确的是(
A.$ \triangle A'B'C' $ 与 $ \triangle ABC $ 是位似图形,位似中心是点 $ (1,0) $
B.$ \triangle A'B'C' $ 与 $ \triangle ABC $ 是位似图形,位似中心是点 $ (0,0) $
C.$ \triangle A'B'C' $ 与 $ \triangle ABC $ 是相似图形,但不是位似图形
D.$ \triangle A'B'C' $ 与 $ \triangle ABC $ 不是相似图形
B
)A.$ \triangle A'B'C' $ 与 $ \triangle ABC $ 是位似图形,位似中心是点 $ (1,0) $
B.$ \triangle A'B'C' $ 与 $ \triangle ABC $ 是位似图形,位似中心是点 $ (0,0) $
C.$ \triangle A'B'C' $ 与 $ \triangle ABC $ 是相似图形,但不是位似图形
D.$ \triangle A'B'C' $ 与 $ \triangle ABC $ 不是相似图形
答案:
B
6. 如图,梯形 $ ABCD $ 的对角线 $ AC $,$ BD $ 相交于点 $ O $,$ G $ 是 $ BD $ 的中点. 若 $ AD = 3 $,$ BC = 9 $,则 $ GO : BG = $(
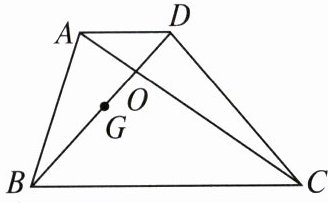
A.$ 1 : 2 $
B.$ 1 : 3 $
C.$ 2 : 3 $
D.$ 11 : 20 $
A
)
A.$ 1 : 2 $
B.$ 1 : 3 $
C.$ 2 : 3 $
D.$ 11 : 20 $
答案:
A 根据△AOD∽△COB,可以知道$\frac{OD}{OB}=\frac{AD}{BC}=\frac{1}{3}$.由于G是BD的中点,从而可以得到GO:BG=1:2.
查看更多完整答案,请扫码查看


