15. 已知抛物线 $ y = -x^{2}+4x - 3 $ 与 $ x $ 轴相交于 $ A,B $ 两点 (点 $ A $ 在点 $ B $ 的左侧), 顶点为 $ P $.
(1) 求 $ A,B,P $ 三点的坐标;
(2) 在给出的平面直角坐标系内画出此抛物线的简图, 并根据简图写出当 $ x $ 取何值时, 函数值 $ y $ 大于零;
(3) 确定此抛物线与直线 $ y = -2x + 6 $ 公共点的个数, 并说明理由.
(1) 求 $ A,B,P $ 三点的坐标;
(2) 在给出的平面直角坐标系内画出此抛物线的简图, 并根据简图写出当 $ x $ 取何值时, 函数值 $ y $ 大于零;
(3) 确定此抛物线与直线 $ y = -2x + 6 $ 公共点的个数, 并说明理由.
答案:
(1)令y = 0,解方程 - x² + 4x - 3 = 0,得x₁ = 1,x₂ = 3,则A(1,0),B(3,0).将y = - x² + 4x - 3配方得y = - (x - 2)² + 1,得顶点P(2,1).
(2)如图,当1 < x < 3时,y > 0.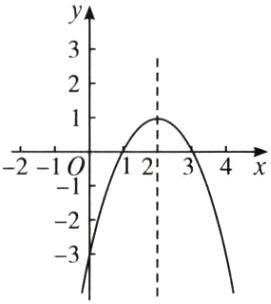
(3)由题意列方程组$\begin{cases} y = - x² + 4x - 3, \\ y = - 2x + 6, \end{cases}$转化为一元二次方程,得x² - 6x + 9 = 0,由Δ = 0,可知方程的两根相等,因此抛物线与直线有唯一的公共点.
(1)令y = 0,解方程 - x² + 4x - 3 = 0,得x₁ = 1,x₂ = 3,则A(1,0),B(3,0).将y = - x² + 4x - 3配方得y = - (x - 2)² + 1,得顶点P(2,1).
(2)如图,当1 < x < 3时,y > 0.

(3)由题意列方程组$\begin{cases} y = - x² + 4x - 3, \\ y = - 2x + 6, \end{cases}$转化为一元二次方程,得x² - 6x + 9 = 0,由Δ = 0,可知方程的两根相等,因此抛物线与直线有唯一的公共点.
16. 某商品的进价为 $ 20 $ 元每件, 售价为 $ 25 $ 元每件时, 每天可卖出 $ 250 $ 件. 市场调查反映, 如果调整价格, 一件商品每涨价 $ 1 $ 元, 那么每天要少卖出 $ 10 $ 件.
(1) 求出每天所得的销售利润 $ w $ (单位: 元) 与每件涨价 $ x $ (单位: 元) 之间的函数解析式;
(2) 求销售单价为多少元时, 该商品每天的销售利润最大;
(3) 商场的营销部在调控价格方面, 提出了 $ A,B $ 两种营销方案.
方案 $ A $: 每件商品涨价不超过 $ 5 $ 元;
方案 $ B $: 每件商品的利润至少为 $ 16 $ 元.
请比较哪种方案的最大利润更高, 并说明理由.
(1) 求出每天所得的销售利润 $ w $ (单位: 元) 与每件涨价 $ x $ (单位: 元) 之间的函数解析式;
(2) 求销售单价为多少元时, 该商品每天的销售利润最大;
(3) 商场的营销部在调控价格方面, 提出了 $ A,B $ 两种营销方案.
方案 $ A $: 每件商品涨价不超过 $ 5 $ 元;
方案 $ B $: 每件商品的利润至少为 $ 16 $ 元.
请比较哪种方案的最大利润更高, 并说明理由.
答案:
(1)根据题意,得w = (25 + x - 20)(250 - 10x),即w = - 10x² + 200x + 1250(0≤x≤25)或w = - 10(x - 10)² + 2250(0≤x≤25).
(2)因为 - 10 < 0,抛物线开口向下,所以二次函数有最大值,当x = - $\frac{b}{2a}$ = - $\frac{200}{2×(- 10)}$ = 10时,销售利润最大,此时销售单价为10 + 25 = 35(元).答:当销售单价为35元时,该商品每天的销售利润最大.
(3)由
(2)可知,抛物线的对称轴为直线x = 10,开口向下,对称轴左侧w随x的增大而增大,对称轴右侧w随x的增大而减小.方案A:根据题意得,x≤5,即0≤x≤5.当x = 5时,利润最大,最大利润为w = - 10×5² + 200×5 + 1250 = 2000(元).方案B:根据题意得,25 + x - 20≥16,x≥11,即11≤x≤25.当x = 11时,利润最大,最大利润为w = - 10×11² + 200×11 + 1250 = 2240(元).因为2240 > 2000,所以方案B最大利润更高.
(1)根据题意,得w = (25 + x - 20)(250 - 10x),即w = - 10x² + 200x + 1250(0≤x≤25)或w = - 10(x - 10)² + 2250(0≤x≤25).
(2)因为 - 10 < 0,抛物线开口向下,所以二次函数有最大值,当x = - $\frac{b}{2a}$ = - $\frac{200}{2×(- 10)}$ = 10时,销售利润最大,此时销售单价为10 + 25 = 35(元).答:当销售单价为35元时,该商品每天的销售利润最大.
(3)由
(2)可知,抛物线的对称轴为直线x = 10,开口向下,对称轴左侧w随x的增大而增大,对称轴右侧w随x的增大而减小.方案A:根据题意得,x≤5,即0≤x≤5.当x = 5时,利润最大,最大利润为w = - 10×5² + 200×5 + 1250 = 2000(元).方案B:根据题意得,25 + x - 20≥16,x≥11,即11≤x≤25.当x = 11时,利润最大,最大利润为w = - 10×11² + 200×11 + 1250 = 2240(元).因为2240 > 2000,所以方案B最大利润更高.
查看更多完整答案,请扫码查看


