《2025年初中同步测控优化设计九年级数学全一册人教版》

14. 如图,在同一平面直角坐标系中有 $5$ 个点：$A(1,1)$,$B(-3,-1)$,$C(-3,1)$,$D(-2,-2)$,$E(0,-3)$.

(1) 画出$\triangle ABC$ 的外接圆$\odot P$,并指出点 $D$ 与$\odot P$ 的位置关系；
(2) 若直线 $l$ 经过点 $D(-2,-2)$,$E(0,-3)$,判断直线 $l$ 与$\odot P$ 的位置关系.

答案：

(1)所画⊙P如图所示.由图可知,⊙P的半径为$\sqrt{5}$.连接PD,
∵PD=$\sqrt{1²+2²}=\sqrt{5}$,
∴点D在⊙P上.
(2)直线l与⊙P相切.理由如下:连接PE.因为直线l过点D(-2,-2),E(0,-3),所以PE²=1²+3²=10,PD²=5,DE²=5,所以PE²=PD²+DE².所以△PDE是直角三角形,且∠PDE=90°.所以PD⊥l.故直线l与⊙P相切.

15. 已知 $BC$ 是$\odot O$ 的直径,点 $D$ 是 $BC$ 延长线上一点,$AB = AD$,$AE$ 是$\odot O$ 的弦,$\angle AEC = 30^{\circ}$.

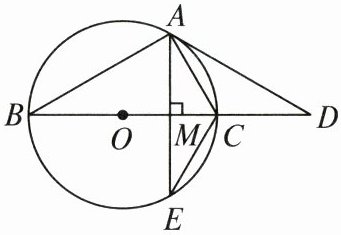
(1) 求证：直线 $AD$ 是$\odot O$ 的切线；
(2) 若 $AE \perp BC$,垂足为点 $M$,$\odot O$ 的半径为 $4$,求 $AE$ 的长.

答案：

(1)证明 连接OA,
∵∠AEC=30°,
∴∠ABC=30°.
∵AB=AD,
∴∠D=∠ABC=30°.
∴∠BAD=120°.
∵OA=OB,
∴∠OAB=∠ABC=30°.
∴∠OAD=∠BAD - ∠OAB=90°.
∴OA⊥AD.
∵点A在⊙O上,
∴直线AD是⊙O的切线.
(2)解
∵∠AEC=30°,
∴∠AOC=60°.
∵BC⊥AE于点M,
∴AE=2AM,∠OMA=90°.在Rt△AOM中,OM=2,AM=$2\sqrt{3}$,
∴AE=2AM=$4\sqrt{3}$.