《2025年初中同步测控优化设计九年级数学全一册人教版》

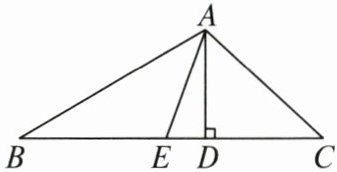
15. 如图,在$\bigtriangleup ABC$中,$AD是BC$边上的高,$AE是BC$边上的中线,$\angle C = 45^{\circ}$,$\sin B = \frac{1}{3}$,$AD = 1$.
(1)求$BC$的长；
(2)求$\tan\angle DAE$的值.

答案：
(1)$\because AD$是BC边上的高，
$\therefore AD\perp BC$.
在$Rt\triangle ABD$中，$\because\sin B=\frac{AD}{AB}=\frac{1}{3}$，$AD=1$，$\therefore AB=3$，$\therefore BD=\sqrt{3^{2}-1^{2}}=2\sqrt{2}$.
在$Rt\triangle ADC$中，$\because\angle C=45^{\circ}$，$\therefore CD=AD=1$.
$\therefore BC=BD+CD=2\sqrt{2}+1$.
(2)$\because AE$是BC边上的中线，
$\therefore DE=CE-CD=\frac{1}{2}BC-CD=\frac{2\sqrt{2}+1}{2}-1=\sqrt{2}-\frac{1}{2}$.
在$Rt\triangle ADE$中，$\tan\angle DAE=\frac{DE}{AD}=\frac{\sqrt{2}-\frac{1}{2}}{1}=\sqrt{2}-\frac{1}{2}$.

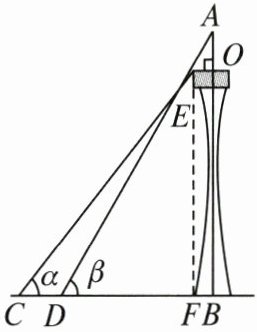
16. 如图,某塔观光层的最外沿点$E$为蹦极项目的起跳点,已知点$E离塔的中轴线AB的距离OE为10m$,塔高$AB为123m$($AB垂直地面BC$),在地面$C处测得点E的仰角\alpha = 45^{\circ}$,从点$C沿CB方向前行40m到达点D$,在点$D处测得塔尖A的仰角\beta = 60^{\circ}$,求点$E离地面的高度EF$.(结果精确到$1m$,参考数据$\sqrt{2} \approx 1.4$,$\sqrt{3} \approx 1.7$)

答案： 在$Rt\triangle ADB$中，$\because\tan\beta=\frac{AB}{BD}$，
$\therefore BD=\frac{AB}{\tan\beta}=\frac{123}{\tan60^{\circ}}=41\sqrt{3}(m)$.
$\therefore DF=BD-BF=(41\sqrt{3}-10)m$.
在$Rt\triangle CEF$中，$\because\tan\alpha=\frac{EF}{CF}$，
$\therefore CF=\frac{EF}{\tan\alpha}=\frac{EF}{\tan45^{\circ}}=EF$.
$\because CF=CD+DF$，
$\therefore CF=40+41\sqrt{3}-10=(41\sqrt{3}+30)m$.
又$EF=CF$，
$\therefore EF=41\sqrt{3}+30\approx100(m)$，
即点E离地面的高度EF约为100 m.