8. 在野外生存训练中,第一小组从营地出发向北偏东$60^{\circ}方向前进了3km$,第二小组向南偏东$30^{\circ}方向前进了3km$,第一小组准备向第二小组靠拢,则行走方向和距离分别为( )
A.南偏西$15^{\circ}$,$3\sqrt{2}km$
B.北偏东$15^{\circ}$,$3\sqrt{2}km$
C.南偏西$15^{\circ}$,$3km$
D.南偏西$45^{\circ}$,$3\sqrt{2}km$
A.南偏西$15^{\circ}$,$3\sqrt{2}km$
B.北偏东$15^{\circ}$,$3\sqrt{2}km$
C.南偏西$15^{\circ}$,$3km$
D.南偏西$45^{\circ}$,$3\sqrt{2}km$
答案:
A 如图,$\triangle ABC$是等腰直角三角形,所以$\angle ABC=45^{\circ}$,$\angle DBC=75^{\circ}$,$BC=3\sqrt{2}\ km$.
所以行走方向为南偏西$15^{\circ}$,距离为$3\sqrt{2}\ km$.

A 如图,$\triangle ABC$是等腰直角三角形,所以$\angle ABC=45^{\circ}$,$\angle DBC=75^{\circ}$,$BC=3\sqrt{2}\ km$.
所以行走方向为南偏西$15^{\circ}$,距离为$3\sqrt{2}\ km$.

9. 已知长为$4m的梯子搭在墙上与地面成45^{\circ}$角,若作业时调整为$60^{\circ}$角(如图所示),则梯子的顶端在垂直方向上沿墙面增加了

$2(\sqrt{3}-\sqrt{2})$
$m$.
答案:
$2(\sqrt{3}-\sqrt{2})$ 4 m的梯子、地面和墙面构成了直角三角形,当梯子搭在墙上与地面成$45^{\circ}$角时,梯子的顶端到地面的距离是$4×\sin45^{\circ}=2\sqrt{2}(m)$.当梯子搭在墙上与地面成$60^{\circ}$角时,梯子的顶端到地面的距离是$4×\sin60^{\circ}=2\sqrt{3}(m)$.故梯子的顶端在垂直方向上沿墙面增加了$2(\sqrt{3}-\sqrt{2})m$.
10. 如图,在网格中,小正方形的边长均为$1$,点$A$,$B$,$C$都在格点上,则$\angle ABC$的正切值是

$\frac{1}{2}$
.
答案:
$\frac{1}{2}$
11. 如图,正方形$ABCD的边长为4$,点$M在边DC$上,$M$,$N两点关于对角线AC$对称.若$DM = 1$,则$\tan\angle ADN = $

$\frac{4}{3}$
.
答案:
$\frac{4}{3}$ 由题知$AD// BC$,则$\angle ADN=\angle DNC$.
$\because$正方形的边长为4,M,N两点关于对角线AC对称,$DM = 1$,$\therefore MC=NC=3$.
$\because CD=4$,
$\therefore\tan\angle ADN=\tan\angle DNC=\frac{CD}{NC}=\frac{4}{3}$.
$\because$正方形的边长为4,M,N两点关于对角线AC对称,$DM = 1$,$\therefore MC=NC=3$.
$\because CD=4$,
$\therefore\tan\angle ADN=\tan\angle DNC=\frac{CD}{NC}=\frac{4}{3}$.
12. 人字梯为现代家庭常用的工具(如图).若$AB$,$AC的长都为2m$,当$\alpha = 50^{\circ}$时,人字梯顶端离地面的高度$AD$是______$m$.(结果精确到$0.1m$,参考依据:$\sin 50^{\circ} \approx 0.77$,$\cos 50^{\circ} \approx 0.64$,$\tan 50^{\circ} \approx 1.19$)


1.5
答案:
1.5
13. 如图,将$45^{\circ}的\angle AOB$按下面的方式放置在一把刻度尺上:顶点$O$与刻度尺下沿的端点重合,$OA$与刻度尺下沿重合,$OB与刻度尺上沿的交点B在刻度尺上的读数恰为2cm$.若按相同的方式将$37^{\circ}的\angle AOC$放置在该刻度尺上,则$OC与刻度尺上沿的交点C$在刻度尺上的读数约为______$cm$.(结果精确到$0.1cm$,参考数据:$\sin 37^{\circ} \approx 0.60$,$\cos 37^{\circ} \approx 0.80$,$\tan 37^{\circ} \approx 0.75$)
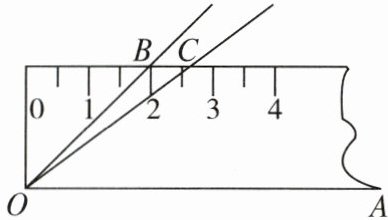

2.7
答案:
2.7
14. 计算:
(1)$\sin^{2}45^{\circ} + \tan 60^{\circ}\cos 30^{\circ} - \tan 45^{\circ}$;
(2)$| - \sqrt{2}| + \cos 60^{\circ} - \tan 30^{\circ} + \sqrt{8}$.
(1)$\sin^{2}45^{\circ} + \tan 60^{\circ}\cos 30^{\circ} - \tan 45^{\circ}$;
(2)$| - \sqrt{2}| + \cos 60^{\circ} - \tan 30^{\circ} + \sqrt{8}$.
答案:
(1)原式$=\left(\frac{\sqrt{2}}{2}\right)^{2}+\sqrt{3}×\frac{\sqrt{3}}{2}-1=\frac{1}{2}+\frac{3}{2}-1=1$;
(2)$|-\sqrt{2}|+\cos60^{\circ}-\tan30^{\circ}+\sqrt{8}=\sqrt{2}+\frac{1}{2}-\frac{\sqrt{3}}{3}+2\sqrt{2}=\frac{1}{2}-\frac{\sqrt{3}}{3}+3\sqrt{2}$.
(1)原式$=\left(\frac{\sqrt{2}}{2}\right)^{2}+\sqrt{3}×\frac{\sqrt{3}}{2}-1=\frac{1}{2}+\frac{3}{2}-1=1$;
(2)$|-\sqrt{2}|+\cos60^{\circ}-\tan30^{\circ}+\sqrt{8}=\sqrt{2}+\frac{1}{2}-\frac{\sqrt{3}}{3}+2\sqrt{2}=\frac{1}{2}-\frac{\sqrt{3}}{3}+3\sqrt{2}$.
查看更多完整答案,请扫码查看


