《2025年初中同步测控优化设计九年级数学全一册人教版》

14. 如图,方格纸中有一条美丽可爱的小金鱼.
(1) 在同一方格纸中,画出将小金鱼图案绕原点 $ O $ 旋转 $ 180^{\circ} $ 后得到的图案；
(2) 在同一方格纸中,并在 $ y $ 轴的右侧,将原小金鱼图案以原点 $ O $ 为位似中心放大,使它们的相似比为 $ 2 : 1 $,画出放大后小金鱼的图案.

答案：
解 如图所示.

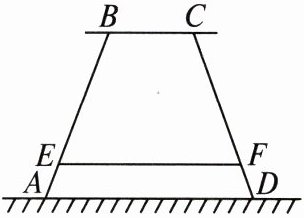
15. 某高中为高一新生设计的学生板凳从侧面看到的图形如图所示. 其中 $ BA = CD $,$ BC = 20 \, cm $,$ BC $,$ EF $ 平行于地面 $ AD $ 且到地面 $ AD $ 的距离分别为 $ 40 \, cm $,$ 8 \, cm $,若使板凳两腿底端 $ A $,$ D $ 之间的距离为 $ 50 \, cm $,则横梁 $ EF $ 的长应为多少？(材质及其厚度等暂忽略不计)

答案：
解 过点C作CM//AB,交EF,AD于点N,M,作CP⊥AD,交EF,AD于点Q,P. 由题意得,四边形ABCM是平行四边形,
∴EN=AM=BC=20cm.
∴MD=AD-AM=50-20=30(cm).由题意知CP=40cm,PQ=8cm,
∴CQ=32cm.
∵EF//AD,
∴△CNF∽△CMD.
∴$\frac{NF}{MD}=\frac{CQ}{CP}$,即$\frac{NF}{30}=\frac{32}{40}$,解得NF=24cm.
∴EF=EN+NF=20+24=44(cm),即横梁EF的长应为44cm.

16. 如图,在 $ \triangle ABC $ 中,延长 $ BC $ 到点 $ D $,使 $ CD = BC $. 取 $ AB $ 的中点 $ F $,连接 $ FD $ 交 $ AC $ 于点 $ E $.

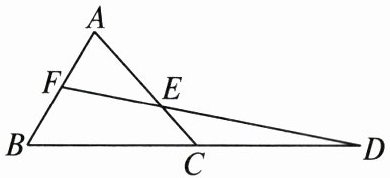
(1) 求 $ \frac{AE}{AC} $ 的值；
(2) 若 $ AB = a $,$ FB = EC $,求 $ AC $ 的长.

答案：
解
(1)过点F作FM//AC,交BC于点M.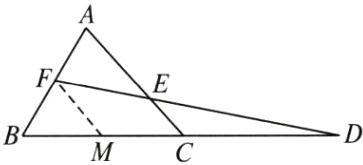
∵F为AB的中点,
∴M为BC的中点,即FM//AC,且$FM=\frac{1}{2}AC$.由FM//AC,得△FMD∽△ECD.
∴$\frac{DC}{DM}=\frac{EC}{FM}=\frac{2}{3}$,
∴$EC=\frac{2}{3}FM=\frac{2}{3}×\frac{1}{2}AC=\frac{1}{3}AC$.
∴$\frac{AE}{AC}=\frac{AC-EC}{AC}=\frac{AC-\frac{1}{3}AC}{AC}=\frac{2}{3}$.
(2)
∵AB=a,
∴$FB=\frac{1}{2}AB=\frac{1}{2}a$.又FB=EC,
∴$EC=\frac{1}{2}a$.
∵$EC=\frac{1}{3}AC$,
∴$AC=3EC=\frac{3}{2}a$.