6. 如图,在平面直角坐标系中,点 $P$ 在第一象限,$\odot P$ 与 $x$ 轴、$y$ 轴都相切,且经过矩形 $AOBC$ 的顶点 $C$,与 $BC$ 相交于点 $D$. 若$\odot P$ 的半径为 $5$,点 $A$ 的坐标是$(0,8)$. 则点 $D$ 的坐标是(

A.$(9,2)$
B.$(9,3)$
C.$(10,2)$
D.$(10,3)$
A
)
A.$(9,2)$
B.$(9,3)$
C.$(10,2)$
D.$(10,3)$
答案:
A
7. 如图,点 $P$ 是等边三角形 $ABC$ 外接圆$\odot O$上的点,在下列判断中,不正确的是(

A.当弦 $PB$ 最长时,$\triangle APC$ 是等腰三角形
B.当$\triangle APC$ 是等腰三角形时,$PO \perp AC$
C.当 $PO \perp AC$ 时,$\angle ACP = 30^{\circ}$
D.当$\angle ACP = 30^{\circ}$时,$\triangle BPC$ 是直角三角形
C
)
A.当弦 $PB$ 最长时,$\triangle APC$ 是等腰三角形
B.当$\triangle APC$ 是等腰三角形时,$PO \perp AC$
C.当 $PO \perp AC$ 时,$\angle ACP = 30^{\circ}$
D.当$\angle ACP = 30^{\circ}$时,$\triangle BPC$ 是直角三角形
答案:
C 对于选项A,当弦PB最长时,PB是⊙O的直径,O既是等边三角形ABC的内心,也是外心,所以∠ABP=∠CBP,根据圆周角性质,$\overset{\frown}{PA}=\overset{\frown}{PC}$,所以PA=PC;对于选项B,当△APC是等腰三角形时,点P是$\overset{\frown}{AC}$的中点或与点B重合,由垂径定理,都可以得到PO⊥AC;对于选项C,当PO⊥AC时,由点P是$\overset{\frown}{AC}$的中点或与点B重合,易得∠ACP=30°或∠ACP=60°;对于选项D,当∠ACP=30°时,分两种情况,点P是$\overset{\frown}{AC}$或$\overset{\frown}{AB}$的中点,都可以得到△BPC是直角三角形.
8. 如图,以等边三角形 $ABC$ 的 $BC$ 边为直径画半圆,分别交 $AB$,$AC$ 于点 $E$,$D$,$DF$ 是圆 $O$ 的切线,过点 $F$ 作 $BC$ 的垂线交 $BC$ 于点 $G$. 若 $AF$ 的长为 $2$,则 $FG$ 的长为(

A.$4$
B.$3\sqrt{3}$
C.$6$
D.$2\sqrt{3}$
B
)
A.$4$
B.$3\sqrt{3}$
C.$6$
D.$2\sqrt{3}$
答案:
B 连接OD,因为DF为圆O的切线,所以OD⊥DF.因为△ABC为等边三角形,所以AB=BC=AC,∠A=∠B=∠C=60°.因为OD=OC,所以△OCD为等边三角形.所以OD//AB.所以DF⊥AB.又O为BC的中点,所以D为AC的中点.在Rt△AFD中,∠ADF=30°,AF=2,所以AD=4,即AC=8.所以FB=AB - AF=8 - 2=6.在Rt△BFG中,∠BFG=30°,所以BG=3,则根据勾股定理得FG=$3\sqrt{3}$,故选B.
9. 如图,点 $A$,$B$,$C$ 在半径为 $9$ 的$\odot O$ 上,$\overset{\frown}{AB}$ 的长为 $2\pi$,则$\angle ACB$ 的大小是 ______.


20°
答案:
20° 连接OA,OB.设∠AOB=n°.
∵$\overset{\frown}{AB}$的长为2π,
∴$\frac{nπ×9}{180}=2π$.
∴n=40,
∴∠AOB=40°.
∴∠ACB=$\frac{1}{2}$∠AOB=20°.
∵$\overset{\frown}{AB}$的长为2π,
∴$\frac{nπ×9}{180}=2π$.
∴n=40,
∴∠AOB=40°.
∴∠ACB=$\frac{1}{2}$∠AOB=20°.
10. 如图,点 $A$,$B$,$C$ 在$\odot O$ 上,$CD \perp OA$,$CE \perp OB$,垂足分别为 $D$,$E$,若$\angle DCE = 40^{\circ}$,则$\angle ACB$ 的度数为
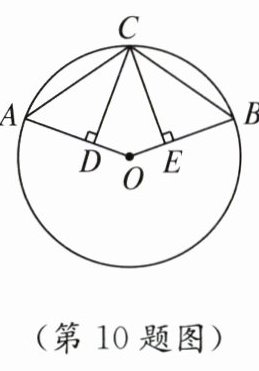
110°
.
答案:
110°
11. 如图,在$\odot O$ 的内接五边形 $ABCDE$ 中,$\angle CAD = 35^{\circ}$,则$\angle B + \angle E = $
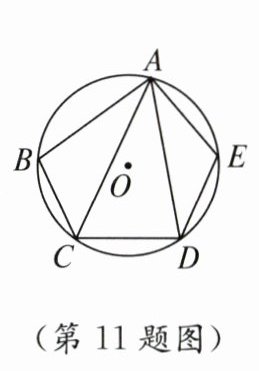
215
$^{\circ}$.
答案:
215 在圆内接四边形ABCD中,∠B+∠ADC=180°,∠B=180° - ∠ADC.在圆内接四边形ACDE中,∠E+∠ACD=180°,∠E=180° - ∠ACD,故∠B+∠E=180° - ∠ADC+180° - ∠ACD=180°+(180° - ∠ADC - ∠ACD)=180°+∠CAD=180°+35°=215°.
12. 如图,$AB$ 为$\odot O$ 的直径,$C$ 为$\odot O$ 外一点,过点 $C$ 作$\odot O$ 的切线,切点为 $B$,连接 $AC$ 交$\odot O$ 于点 $D$,$\angle C = 38^{\circ}$. 点 $E$ 在 $AB$ 右侧的半圆周上运动(不与 $A$,$B$ 重合),则$\angle AED$ 的度数为 ______.


38°
答案:
38° 如图,连接BE,则直径AB所对的圆周角∠AEB=90°.由BC是⊙O的切线得∠ABC=90°,∠BAC=90° - ∠C=90° - 38°=52°.因为∠BAC=∠BED=52°,所以∠AED=∠AEB - ∠BED=90° - 52°=38°.
13. 如图,$AB$,$AC$ 分别是$\odot O$ 的直径和弦,$OD \perp AC$,垂足为 $D$,连接 $BD$,$BC$,$AB = 5$,$AC = 4$,则 $BD = $
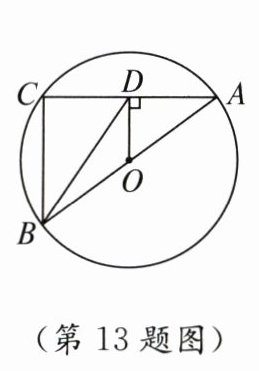
$\sqrt{13}$
.
答案:
$\sqrt{13}$ 由垂径定理,得CD=2,由AB是⊙O的直径,得∠C=90°.由勾股定理,得BC=3,在Rt△BCD中,由勾股定理得BD=$\sqrt{13}$.
查看更多完整答案,请扫码查看


