16. 如图,已知在$\odot O$ 中,$AB = 4\sqrt{3}$,$AC$ 是$\odot O$ 的直径,$AC \perp BD$,垂足为 $F$,$\angle A = 30^{\circ}$.
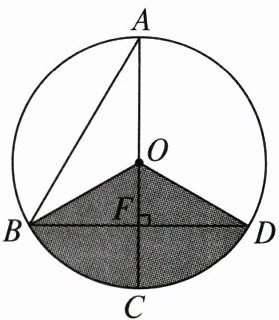
(1) 求图中阴影部分的面积;
(2) 若用阴影扇形 $OBD$ 围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.

(1) 求图中阴影部分的面积;
(2) 若用阴影扇形 $OBD$ 围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.
答案:
(1)在Rt△ABF中,∠A=30°,则BF=$\frac{1}{2}$AB=$2\sqrt{3}$,于是AF=$\sqrt{(4\sqrt{3})²-(2\sqrt{3})²}=6$.在Rt△BOF中,OB²=OF²+BF²=(AF - OA)²+BF²,又OB=OA,
∴OA²=(6 - OA)²+(2$\sqrt{3}$)².
∴OA=4.
∵∠BAO=30°,
∴∠BOF=2∠BAO=60°.又OB=OD,OC⊥BD,
∴∠BOD=2∠BOF=120°.
∴S${}_{阴影}$=$\frac{120π×4²}{360}=\frac{16π}{3}$.
(2)设圆锥的底面圆的半径为r,则2πr=$\frac{120×4π}{180}$,解得r=$\frac{4}{3}$.
(1)在Rt△ABF中,∠A=30°,则BF=$\frac{1}{2}$AB=$2\sqrt{3}$,于是AF=$\sqrt{(4\sqrt{3})²-(2\sqrt{3})²}=6$.在Rt△BOF中,OB²=OF²+BF²=(AF - OA)²+BF²,又OB=OA,
∴OA²=(6 - OA)²+(2$\sqrt{3}$)².
∴OA=4.
∵∠BAO=30°,
∴∠BOF=2∠BAO=60°.又OB=OD,OC⊥BD,
∴∠BOD=2∠BOF=120°.
∴S${}_{阴影}$=$\frac{120π×4²}{360}=\frac{16π}{3}$.
(2)设圆锥的底面圆的半径为r,则2πr=$\frac{120×4π}{180}$,解得r=$\frac{4}{3}$.
17. 如图,已知$\triangle ABC$ 内接于$\odot O$,$AB$ 是$\odot O$ 的直径,$\odot O$ 的切线 $PC$ 交 $BA$ 的延长线于点 $P$,$OF // BC$,$OF$ 交 $AC$ 于点 $E$,交 $PC$ 于点 $F$,连接 $AF$.
(1) 判断 $AF$ 与$\odot O$ 的位置关系并说明理由;
(2) 若$\odot O$ 的半径为 $4$,$AF = 3$,求 $AC$ 的长.
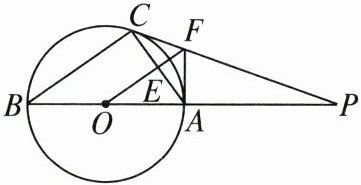
(1) 判断 $AF$ 与$\odot O$ 的位置关系并说明理由;
(2) 若$\odot O$ 的半径为 $4$,$AF = 3$,求 $AC$ 的长.

答案:
(1)AF是⊙O的切线.理由如下:连接OC,
∵AB是⊙O的直径,
∴∠BCA=90°.
∵OF//BC,
∴∠AEO=90°,即OF⊥AC.
∵OC=OA,
∴∠COF=∠AOF,
∴△OCF≌△OAF.
∴∠OAF=∠OCF=90°,
∴FA⊥OA,即AF是⊙O的切线.
(2)
∵⊙O的半径为4,AF=3,FA⊥OA,
∴OF=$\sqrt{AF²+OA²}=\sqrt{3²+4²}=5$.
∵FA⊥OA,OF⊥AC,
∴AF·OA=OF·EA,
∴3×4=5EA,解得AE=$\frac{12}{5}$,AC=2AE=$\frac{24}{5}$.
(1)AF是⊙O的切线.理由如下:连接OC,
∵AB是⊙O的直径,
∴∠BCA=90°.
∵OF//BC,
∴∠AEO=90°,即OF⊥AC.
∵OC=OA,
∴∠COF=∠AOF,
∴△OCF≌△OAF.
∴∠OAF=∠OCF=90°,
∴FA⊥OA,即AF是⊙O的切线.
(2)
∵⊙O的半径为4,AF=3,FA⊥OA,
∴OF=$\sqrt{AF²+OA²}=\sqrt{3²+4²}=5$.
∵FA⊥OA,OF⊥AC,
∴AF·OA=OF·EA,
∴3×4=5EA,解得AE=$\frac{12}{5}$,AC=2AE=$\frac{24}{5}$.
查看更多完整答案,请扫码查看


