《2025年作业本浙江教育出版社六年级数学上册北师大版》

(1) 分别将车轮做成下面三种形状,滚动起来最平稳的是(C)。

答案： 解析：本题考查圆的特征。圆是平面内到定点的距离等于定长的所有点的集合，圆上任意一点到圆心的距离都相等，当车轮做成圆形时，车轴到地面的距离就等于圆的半径，在滚动过程中这个距离始终保持不变，所以滚动起来最平稳。而三角形和正方形的中心到各边的距离不相等，滚动时车轴到地面的距离会不断变化，滚动起来就不平稳。
答案：C。

(2) 在一个边长是$6cm$的正方形中画一个最大的圆,则这个圆的半径是(A)cm。
A.3
B.6
C.4

答案： 分析：
在一个边长为$6cm$的正方形中画一个最大的圆，要使圆最大，则圆的直径必须等于正方形的边长。
因为圆的半径是直径的一半，所以我们可以通过将正方形的边长除以2来得到圆的半径。
根据以上分析，我们可以建立以下数学模型：
圆的直径 = 正方形的边长 = $6cm$。
圆的半径 = 圆的直径 $÷$ 2。
圆的半径 = $6cm ÷ 2 = 3cm$。
答案：A.$3cm$。

(3) 下列说法正确的是(C)。
A.半径是线段,直径是直线
B.直径比半径长
C.在等圆中,半径是直径的一半

答案： 解析：
本题考查的是对圆的基本性质的理解，包括半径、直径的定义及其关系。
A选项：半径是线段，这是正确的，因为半径是从圆心到圆上任意一点的距离，它有明确的起点和终点，所以是线段。但直径并不是直线，而是经过圆心并且两端都在圆上的线段。因此，A选项是错误的。
B选项：直径比半径长，这个说法不完全准确。在同一个圆或等圆中，直径确实是半径的两倍，所以比半径长。但如果比较的是不同的圆，那么直径和半径的长度关系就不能确定。因此，B选项也是错误的。
C选项：在等圆中，半径是直径的一半，这是准确的。在同一个圆或等圆中，直径是经过圆心的特殊的弦，它的长度是半径的两倍，所以半径确实是直径的一半。
答案：C

(4) 用圆规画圆时,圆规两脚间的距离为4厘米,所画的圆的直径是(C)厘米。
A.2
B.4
C.8

答案： 解析：
本题考查的是对圆的直径的理解以及圆规画圆的基本原理。
圆规两脚间的距离代表的是圆的半径，根据圆的性质，直径是半径的两倍，即 $直径 = 2 × 半径$。
题目中给出圆规两脚间的距离为4厘米，这就是圆的半径。
所以，$直径 = 2 × 4 = 8(厘米)$。
答案：
C

圆的半径是(2cm) 圆的半径是$7cm$
长方形的长是(12cm) 三角形的周长是(42cm)

答案： 解析：本题主要考查对圆、长方形和三角形的认识以及周长的计算。
第一个图：
圆的直径等于长方形的宽，为$4cm$，根据半径是直径的一半，可得圆的半径为$4÷2 = 2(cm)$。
长方形的长等于圆的直径的$3$倍，即$4×3 = 12(cm)$。
第二个图：
已知圆的半径是$7cm$。
观察发现，等边三角形的边长等于圆的直径，根据$圆的直径=2×半径$，可得等边三角形的边长为$2×7 = 14(cm)$。
再根据$等边三角形的周长=边长×3$，可得三角形的周长为$14×3 = 42(cm)$。
答案：$2cm$；$12cm$；$42cm$。

3. 先画一画,再回答问题。
在下面这个长$5cm$、宽$4cm$的长方形中,先画一个最大的正方形,再画一个最大的圆,圆的半径是(2)cm,直径是(4)cm。

答案：
解析：本题主要考查在长方形中画最大的正方形和圆，以及圆的半径和直径的关系。
首先，要在长$5cm$、宽$4cm$的长方形中画一个最大的正方形。
最大的正方形的边长应等于长方形的短边，即$4cm$。
然后，在这个正方形中画一个最大的圆。
最大的圆的直径应等于正方形的边长，即$4cm$。
最后，根据圆的半径是直径的一半，可以计算出圆的半径。
答案：

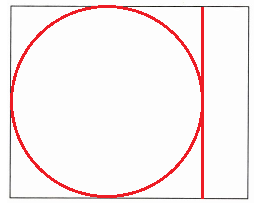
圆的半径是$4 ÷ 2=2(cm)$，直径是$4cm$。
故填：$2$；$4$。