2025年七彩假日快乐假期暑假作业八年级理综
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年七彩假日快乐假期暑假作业八年级理综 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
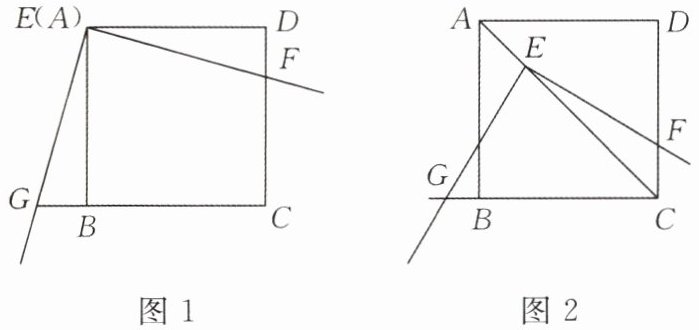
2. 如图 1, 将三角板放在正方形 $ABCD$ 上, 使三角板的直角顶点 $E$ 与正方形 $ABCD$ 的顶点 $A$ 重合, 三角板的一边交 $CD$ 于点 $F$, 另一边交 $CB$ 的延长线于点 $G$.
(1) 求证: $EF = EG$;
(2) 如图 2, 移动三角板, 使顶点 $E$ 始终在正方形 $ABCD$ 的对角线 $AC$ 上, 其他条件不变. (1) 中的结论是否仍然成立? 若成立, 请给予证明; 若不成立, 请说明理由.
思路点拨: 第 (1) 小题可以通过直接证明 $\triangle EDF \cong \triangle EBG$ 求解. 第 (2) 小题是动态画图题, 其证明的思路与第 (1) 小题是类似的, 抓住这一点很重要.
(1) 求证: $EF = EG$;
(2) 如图 2, 移动三角板, 使顶点 $E$ 始终在正方形 $ABCD$ 的对角线 $AC$ 上, 其他条件不变. (1) 中的结论是否仍然成立? 若成立, 请给予证明; 若不成立, 请说明理由.
思路点拨: 第 (1) 小题可以通过直接证明 $\triangle EDF \cong \triangle EBG$ 求解. 第 (2) 小题是动态画图题, 其证明的思路与第 (1) 小题是类似的, 抓住这一点很重要.

答案:
(1) 证明:
∵ $\angle DEF + \angle BEF = 90^{\circ}$, $\angle GEB + \angle BEF = 90^{\circ}$.
∴ $\angle DEF = \angle GEB$.
又
∵ $ED = EB$,
∴ $Rt\triangle EFD \cong Rt\triangle EGB(ASA)$.
∴ $EF = EG$.
(2) 解: 成立. 证明如下: 如图, 过点 $E$ 分别作 $BC$, $CD$ 的垂线, 垂足分别为 $H$, $I$, 则 $EH = EI$, $\angle HEI = 90^{\circ}$.
∵ $\angle IEF + \angle HEF = 90^{\circ}$, $\angle GEH + \angle HEF = 90^{\circ}$,
∴ $\angle IEF = \angle GEH$.
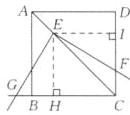
∴ $Rt\triangle FEI \cong Rt\triangle GEH(ASA)$,
∴ $EF = EG$.
(1) 证明:
∵ $\angle DEF + \angle BEF = 90^{\circ}$, $\angle GEB + \angle BEF = 90^{\circ}$.
∴ $\angle DEF = \angle GEB$.
又
∵ $ED = EB$,
∴ $Rt\triangle EFD \cong Rt\triangle EGB(ASA)$.
∴ $EF = EG$.
(2) 解: 成立. 证明如下: 如图, 过点 $E$ 分别作 $BC$, $CD$ 的垂线, 垂足分别为 $H$, $I$, 则 $EH = EI$, $\angle HEI = 90^{\circ}$.
∵ $\angle IEF + \angle HEF = 90^{\circ}$, $\angle GEH + \angle HEF = 90^{\circ}$,
∴ $\angle IEF = \angle GEH$.

∴ $Rt\triangle FEI \cong Rt\triangle GEH(ASA)$,
∴ $EF = EG$.
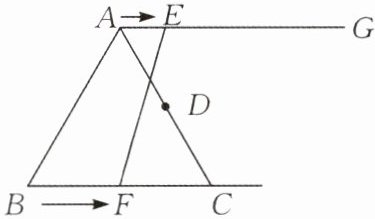
3. 如图, 在等边三角形 $ABC$ 中, $BC = 6\mathrm{cm}$, 射线 $AG // BC$, 点 $E$ 从点 $A$ 出发沿射线 $AG$ 以 $1\mathrm{cm/s}$ 的速度运动, 同时点 $F$ 从点 $B$ 出发沿射线 $BC$ 以 $2\mathrm{cm/s}$ 的速度运动, 设运动时间为 $t$ (单位: $s$).
(1) 连接 $EF$, 当 $EF$ 经过 $AC$ 边的中点 $D$ 时, 求证: $\triangle ADE \cong \triangle CDF$;
(2) 当 $t$ 为多少秒时, 四边形 $ACFE$ 是菱形?
思路点拨: 第 (1) 小题可以直接运用 “$AAS$” 证明 $\triangle ADE \cong \triangle CDF$ 求解. 第 (2) 小题是运动型问题, 假设四边形 $ACFE$ 是菱形, 则有 $AE = AC = CF = EF$, 即可构建关于 $t$ 的方程求解.
(1) 连接 $EF$, 当 $EF$ 经过 $AC$ 边的中点 $D$ 时, 求证: $\triangle ADE \cong \triangle CDF$;
(2) 当 $t$ 为多少秒时, 四边形 $ACFE$ 是菱形?
思路点拨: 第 (1) 小题可以直接运用 “$AAS$” 证明 $\triangle ADE \cong \triangle CDF$ 求解. 第 (2) 小题是运动型问题, 假设四边形 $ACFE$ 是菱形, 则有 $AE = AC = CF = EF$, 即可构建关于 $t$ 的方程求解.

答案:
(1) 略
(2) 解: 当四边形 $ACFE$ 是菱形时, $AE = AC = CF = EF$, 由题意可知, $AE = t$, $CF = 2t - 6$. 又
∵ $\triangle ABC$ 是等边三角形,
∴ $AC = BC = 6(cm)$,
∴ $t = 6$, $2t - 6 = 6$, 即 $t = 6(s)$.
(1) 略
(2) 解: 当四边形 $ACFE$ 是菱形时, $AE = AC = CF = EF$, 由题意可知, $AE = t$, $CF = 2t - 6$. 又
∵ $\triangle ABC$ 是等边三角形,
∴ $AC = BC = 6(cm)$,
∴ $t = 6$, $2t - 6 = 6$, 即 $t = 6(s)$.
查看更多完整答案,请扫码查看


