2025年七彩假日快乐假期暑假作业八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年七彩假日快乐假期暑假作业八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
9.(★★☆☆☆)关于一次函数 $ y = 2x - 1 $ 的图象,下列说法正确的是(
A.图象经过第一、二、三象限
B.图象经过第一、三、四象限
C.图象经过第一、二、四象限
D.图象经过第二、三、四象限
B
)A.图象经过第一、二、三象限
B.图象经过第一、三、四象限
C.图象经过第一、二、四象限
D.图象经过第二、三、四象限
答案:
B
10.(★★☆☆☆)如图,一次函数 $ y_1 = x + b $ 与一次函数 $ y_2 = kx + 4 $ 的图象交于点 $ P(1,3) $,则关于 x 的不等式 $ x + b > kx + 4 $ 的解集是(
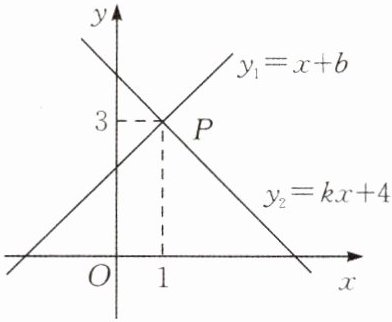
A.$ x > -2 $
B.$ x > 0 $
C.$ x > 1 $
D.$ x < 1 $
C
)
A.$ x > -2 $
B.$ x > 0 $
C.$ x > 1 $
D.$ x < 1 $
答案:
C
11.(★★☆☆☆)某水库的水位在 5 h 内持续上涨,初始水位高度为 6 m,水位以每小时0.3 m的速度匀速上升,则水库的水位 y 与上涨时间 x 之间的函数关系式是
$y = 0.3x + 6(0 \leqslant x \leqslant 5)$
.
答案:
$y = 0.3x + 6(0 \leqslant x \leqslant 5)$
12.(★★☆☆☆)已知直线 $ y = 2x + (3 - a) $ 与 x 轴的交点在 $ A(2,0) $,$ B(3,0) $ 之间(包括 A,B两点),则 a 的取值范围是
$7 \leqslant a \leqslant 9$
.
答案:
$7 \leqslant a \leqslant 9$
13.(★★★☆☆)如图,直线 l 上有一点 $ P_1(2,1) $,将点 $ P_1 $ 先向右平移 1 个单位长度,再向上平移 2 个单位长度得到点 $ P_2 $,点 $ P_2 $ 恰好在直线 l 上.
(1)写出点 $ P_2 $ 的坐标;
(2)求直线 l 所表示的一次函数的表达式;
(3)若将点 $ P_2 $ 先向右平移 3 个单位长度,再向上平移 6 个单位长度得到点 $ P_3 $. 请判断点 $ P_3 $ 是否在直线 l 上,并说明理由.
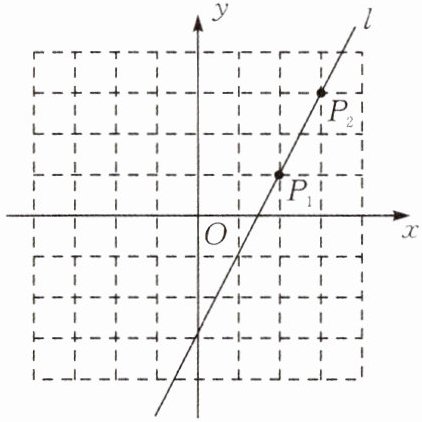
(1)写出点 $ P_2 $ 的坐标;
(3,3)
(2)求直线 l 所表示的一次函数的表达式;
y=2x-3
(3)若将点 $ P_2 $ 先向右平移 3 个单位长度,再向上平移 6 个单位长度得到点 $ P_3 $. 请判断点 $ P_3 $ 是否在直线 l 上,并说明理由.
点$P_3$在直线l上。理由:$P_3$的坐标为$(3+3,3+6)=(6,9)$,当$x=6$时,$y=2×6-3=9$,所以点$P_3$在直线l上

答案:
(1) $P_2(3,3)$
(2) 设直线$l$的表达式为$y=kx+b$,将$P_1(2,1)$,$P_2(3,3)$代入得:
$\begin{cases}2k+b=1\\3k+b=3\end{cases}$
解得$\begin{cases}k=2\\b=-3\end{cases}$
$\therefore$直线$l$的表达式为$y=2x-3$
(3) $P_3$的坐标为$(3+3,3+6)=(6,9)$
当$x=6$时,$y=2×6-3=9$
$\therefore$点$P_3$在直线$l$上
(1) $P_2(3,3)$
(2) 设直线$l$的表达式为$y=kx+b$,将$P_1(2,1)$,$P_2(3,3)$代入得:
$\begin{cases}2k+b=1\\3k+b=3\end{cases}$
解得$\begin{cases}k=2\\b=-3\end{cases}$
$\therefore$直线$l$的表达式为$y=2x-3$
(3) $P_3$的坐标为$(3+3,3+6)=(6,9)$
当$x=6$时,$y=2×6-3=9$
$\therefore$点$P_3$在直线$l$上
确定解析式 常用待定系数法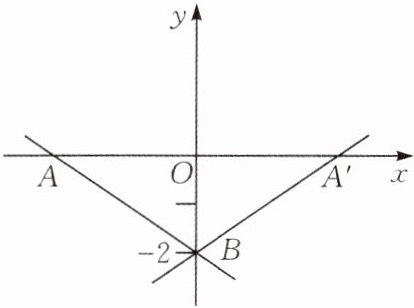
【提出问题】已知一次函数的图象经过点 $ (0,-2) $,且与两坐标轴围成的三角形面积为 3,求这个一次函数的解析式.

【提出问题】已知一次函数的图象经过点 $ (0,-2) $,且与两坐标轴围成的三角形面积为 3,求这个一次函数的解析式.
答案:
【探究问题】题中有两个独立的条件:一个是“图象经过点 $ (0,-2) $”;另一个是“与两坐标轴围成的三角形面积为 3”. 利用已知条件,画出函数图象的示意图,再根据面积公式列方程. 根据已知条件画出一次函数图象的示意图,示意图即为如图所示的直线 AB 或直线 $ A'B $. 设直线与 x 轴的交点坐标为 $ (x,0) $,则有 $ OA = OA' = |x| $,$ OB = |-2| = 2 $. $ \because S_{\triangle OAB} = 3 $,$ \therefore \frac{1}{2}OA \cdot OB = 3 $,即有 $ \frac{1}{2}|x| \cdot 2 = 3 $,解得 $ x = \pm 3 $,$ \therefore A(-3,0) $,$ A'(3,0) $. 设一次函数的解析式为 $ y = kx + b $($ k \neq 0 $). 把点 $ (-3,0) $,$ (0,-2) $ 的坐标代入解析式得 $ \begin{cases} -3k + b = 0 \\ b = -2 \end{cases} $,解得 $ \begin{cases} k = -\frac{2}{3} \\ b = -2 \end{cases} $,$ \therefore y = -\frac{2}{3}x - 2 $.
把点 $ (3,0) $,$ (0,-2) $ 的坐标代入解析式得 $ \begin{cases} 3k + b = 0 \\ b = -2 \end{cases} $,解得 $ \begin{cases} k = \frac{2}{3} \\ b = -2 \end{cases} $,$ \therefore y = \frac{2}{3}x - 2 $.
综上可知,一次函数的解析式为 $ y = -\frac{2}{3}x - 2 $ 或 $ y = \frac{2}{3}x - 2 $.
【方法归纳】待定系数法是指事先设定一些待确定的系数,再根据题意,建立起含有待定字母系数的方程(组),并求出相应字母系数的值,从而使问题得到解决的方法. 待定系数法是一种重要的数学方法,可以运用于因式分解,确定方程的系数,确定函数的解析式,等等. 它的一般步骤:①设定含待定字母系数的解析式;②根据恒等条件,列出含待定字母系数的方程(组);③解方程(组)求出待定字母系数,从而使问题得到圆满解决.
把点 $ (3,0) $,$ (0,-2) $ 的坐标代入解析式得 $ \begin{cases} 3k + b = 0 \\ b = -2 \end{cases} $,解得 $ \begin{cases} k = \frac{2}{3} \\ b = -2 \end{cases} $,$ \therefore y = \frac{2}{3}x - 2 $.
综上可知,一次函数的解析式为 $ y = -\frac{2}{3}x - 2 $ 或 $ y = \frac{2}{3}x - 2 $.
【方法归纳】待定系数法是指事先设定一些待确定的系数,再根据题意,建立起含有待定字母系数的方程(组),并求出相应字母系数的值,从而使问题得到解决的方法. 待定系数法是一种重要的数学方法,可以运用于因式分解,确定方程的系数,确定函数的解析式,等等. 它的一般步骤:①设定含待定字母系数的解析式;②根据恒等条件,列出含待定字母系数的方程(组);③解方程(组)求出待定字母系数,从而使问题得到圆满解决.
查看更多完整答案,请扫码查看


