2025年七彩假日快乐假期暑假作业八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年七彩假日快乐假期暑假作业八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
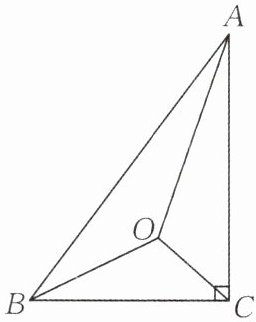
14.(★★★★☆)在$Rt\triangle ABC$中,$∠C= 90^{\circ },AC= 4,BC= 3,∠A,∠B,∠C$三个角的平分线相交于点O,试求点O到三边的距离.
1

答案:
解:设点O到三边的距离为$r$。
在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 4$,$BC = 3$,
由勾股定理得$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{4^{2}+3^{2}} = 5$。
因为点O是$\triangle ABC$三条角平分线的交点,
所以点O到三边的距离相等,均为$r$。
$\triangle ABC$的面积为$\frac{1}{2}× AC× BC=\frac{1}{2}×4×3 = 6$。
又因为$\triangle ABC$的面积还可表示为$\triangle AOB$、$\triangle BOC$、$\triangle AOC$的面积之和,
即$\frac{1}{2}× AB× r+\frac{1}{2}× BC× r+\frac{1}{2}× AC× r$,
所以$\frac{1}{2}×(AB + BC + AC)× r=6$,
即$\frac{1}{2}×(5 + 3 + 4)× r=6$,
$6r=6$,解得$r = 1$。
答:点O到三边的距离为1。
在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 4$,$BC = 3$,
由勾股定理得$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{4^{2}+3^{2}} = 5$。
因为点O是$\triangle ABC$三条角平分线的交点,
所以点O到三边的距离相等,均为$r$。
$\triangle ABC$的面积为$\frac{1}{2}× AC× BC=\frac{1}{2}×4×3 = 6$。
又因为$\triangle ABC$的面积还可表示为$\triangle AOB$、$\triangle BOC$、$\triangle AOC$的面积之和,
即$\frac{1}{2}× AB× r+\frac{1}{2}× BC× r+\frac{1}{2}× AC× r$,
所以$\frac{1}{2}×(AB + BC + AC)× r=6$,
即$\frac{1}{2}×(5 + 3 + 4)× r=6$,
$6r=6$,解得$r = 1$。
答:点O到三边的距离为1。
查看更多完整答案,请扫码查看


