《2025年七彩假日快乐假期暑假作业八年级数学》

【提出问题】如图,在正方形$ABCD$中,点$E$,$F分别为DC$,$BC$边上的点,且满足$∠EAF= 45^{\circ}$,连接$EF$,求证:$DE+BF= EF$.



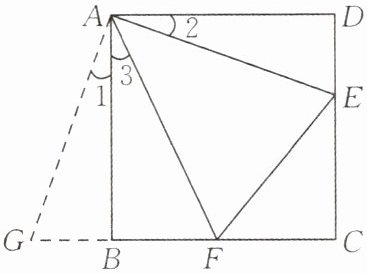
【探究问题】解答此问题的关键是设法运用$∠EAF= 45^{\circ}$.又考虑到本例是证明线段的和差关系,需要截长补短,于是将$\triangle ADE绕点A顺时针旋转90^{\circ}得到\triangle ABG$,此时$AD与AB$重合,由旋转可得:$AB= AD$,$BG= DE$,$∠1= ∠2$,$∠ABG= ∠D= 90^{\circ}$,$\therefore∠ABG+∠ABF= 90^{\circ}+90^{\circ}=180^{\circ}$,因此,点$G$,$B$,$F$在同一条直线上.$\because∠EAF= 45^{\circ}$,$\therefore∠2+∠3= ∠BAD-∠EAF= 90^{\circ}-45^{\circ}=45^{\circ}$.$\because∠1= ∠2$,$\therefore∠1+∠3= 45^{\circ}$,即$∠GAF= ∠EAF$.又$\because AG= AE$,$AF= AF$,$\therefore\triangle GAF≌\triangle EAF$(SAS),$\therefore GF= EF$,故$DE+BF= EF$.
【方法归纳】线段的和差倍分关系的主要证明方法有:(1)截长法,即在较长线段上截取一段等于一较短线段,再证明剩余部分等于另一较短线段;(2)补短法.延长较短线段中的一条,使延长的部分等于另一较短线段,则两较短线段合成一条线段,设法证明该线段等于较长线段.本例采用的是补短法.

答案： 【探究问题】解答此问题的关键是设法运用$∠EAF= 45^{\circ}$.又考虑到本例是证明线段的和差关系,需要截长补短,于是将$\triangle ADE绕点A顺时针旋转90^{\circ}得到\triangle ABG$,此时$AD与AB$重合,由旋转可得:$AB= AD$,$BG= DE$,$∠1= ∠2$,$∠ABG= ∠D= 90^{\circ}$,$\therefore∠ABG+∠ABF= 90^{\circ}+90^{\circ}=180^{\circ}$,因此,点$G$,$B$,$F$在同一条直线上.$\because∠EAF= 45^{\circ}$,$\therefore∠2+∠3= ∠BAD-∠EAF= 90^{\circ}-45^{\circ}=45^{\circ}$.$\because∠1= ∠2$,$\therefore∠1+∠3= 45^{\circ}$,即$∠GAF= ∠EAF$.又$\because AG= AE$,$AF= AF$,$\therefore\triangle GAF≌\triangle EAF(SAS)$,$\therefore GF= EF$,故$DE+BF= EF$.
【方法归纳】线段的和差倍分关系的主要证明方法有:
(1)截长法,即在较长线段上截取一段等于一较短线段,再证明剩余部分等于另一较短线段;
(2)补短法.延长较短线段中的一条,使延长的部分等于另一较短线段,则两较短线段合成一条线段,设法证明该线段等于较长线段.本例采用的是补短法.

12.(★★★★☆)如图,将$Rt\triangle ABC沿斜边翻折得到\triangle ADC$,点$E$,$F分别为DC$,$BC$边上的点,且$∠EAF= \frac{1}{2}∠DAB$.试猜想$DE$,$BF$,$EF$之间有何数量关系,并证明你的猜想.
思路点拨:先利用补短法延长短线段,再证明三条线段之间的数量关系.

猜想：$DE + BF = EF$。
证明：延长 $CB$ 至点 $G$，使 $BG = DE$，连接 $AG$。
因为将 $Rt\triangle ABC$ 沿斜边翻折得到 $\triangle ADC$，所以 $AD = AB$，$\angle ADC = \angle ABC = 90^{\circ}$，$\angle DAB = 2\angle CAB$。
所以 $\angle ABG = 180^{\circ}-\angle ABC = 90^{\circ} = \angle ADE$。
在 $\triangle ADE$ 和 $\triangle ABG$ 中，
$\begin{cases}AD = AB \\\angle ADE = \angle ABG \\DE = BG\end{cases}$
所以 $\triangle ADE \cong \triangle ABG(SAS)$，则 $AE = AG$，$\angle DAE = \angle BAG$。
因为 $\angle EAF = \frac{1}{2}\angle DAB$，所以 $\angle DAE + \angle BAF = \angle EAF$，即 $\angle BAG + \angle BAF = \angle EAF$，所以 $\angle GAF = \angle EAF$。
在 $\triangle AFG$ 和 $\triangle AFE$ 中，
$\begin{cases}AG = AE \\\angle GAF = \angle EAF \\AF = AF\end{cases}$
所以 $\triangle AFG \cong \triangle AFE(SAS)$，则 $GF = EF$。
因为 $GF = BF + BG = BF + DE$，所以$DE + BF = EF$。
结论：$DE + BF = EF$。

答案： 解：猜想：$DE + BF = EF$。
证明：延长 $CB$ 至点 $G$，使 $BG = DE$，连接 $AG$。
因为将 $Rt\triangle ABC$ 沿斜边翻折得到 $\triangle ADC$，所以 $AD = AB$，$\angle ADC = \angle ABC = 90^{\circ}$，$\angle DAB = 2\angle CAB$。
所以 $\angle ABG = 180^{\circ}-\angle ABC = 90^{\circ} = \angle ADE$。
在 $\triangle ADE$ 和 $\triangle ABG$ 中，
$\begin{cases}AD = AB \\\angle ADE = \angle ABG \\DE = BG\end{cases}$
所以 $\triangle ADE \cong \triangle ABG(SAS)$，则 $AE = AG$，$\angle DAE = \angle BAG$。
因为 $\angle EAF = \frac{1}{2}\angle DAB$，所以 $\angle DAE + \angle BAF = \angle EAF$，即 $\angle BAG + \angle BAF = \angle EAF$，所以 $\angle GAF = \angle EAF$。
在 $\triangle AFG$ 和 $\triangle AFE$ 中，
$\begin{cases}AG = AE \\\angle GAF = \angle EAF \\AF = AF\end{cases}$
所以 $\triangle AFG \cong \triangle AFE(SAS)$，则 $GF = EF$。
因为 $GF = BF + BG = BF + DE$，所以 $DE + BF = EF$。
结论：$DE + BF = EF$。