2025年七彩假日快乐假期暑假作业八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年七彩假日快乐假期暑假作业八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
学会构造 巧妙求解
【提出问题】如图,在六边形ABCDEF中,$∠A= ∠B= ∠C= ∠D= ∠E= ∠F= 120^{\circ }$,$AB= 1$,$BC= 3$,$CD= 3$,$DE= 2$,求这个六边形的周长。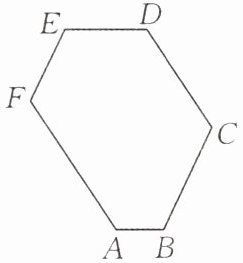
【提出问题】如图,在六边形ABCDEF中,$∠A= ∠B= ∠C= ∠D= ∠E= ∠F= 120^{\circ }$,$AB= 1$,$BC= 3$,$CD= 3$,$DE= 2$,求这个六边形的周长。

答案:
【探究问题】由已知六边形各个内角为$120^{\circ }$,易得其内角的邻补角为$60^{\circ }$,从而联想到作其邻补角,得四边形,易证其为平行四边形,利用平行四边形的性质解决问题。于是,延长BA交EF的延长线于点M,延长BC交ED的延长线于点N。
$\because ∠1= ∠2= 120^{\circ }$,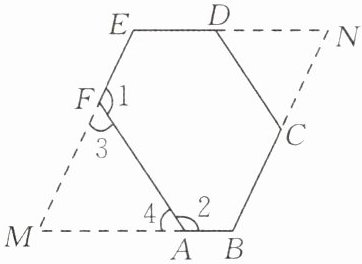
$\therefore ∠3= ∠4= 60^{\circ }$,
$\therefore △MAF$是等边三角形。同理,$△NCD$也是等边三角形。
$\therefore ∠M= ∠N= 60^{\circ }$。
$\because ∠E= ∠B= 120^{\circ }$,
$\therefore ∠M+∠E= ∠M+∠B= 180^{\circ }$,
$\therefore ME// BN$,$MB// EN$,
$\therefore$四边形MBNE为平行四边形,
$\therefore ME= BN$。
$\because FA= FM$,$CD= CN$,
$\therefore EF+FA= BC+CD= 6$,
$\therefore AB+BC+CD+DE+EF+FA= 15$。
【方法归纳】将多边形的问题转化为三角形或四边形的问题不失为一种好方法,本例由题意知各角都为$120^{\circ }$,自然会联想到它的外角都为$60^{\circ }$,如延长各边,能得到等边三角形或平行四边形。当所遇问题中,涉及$120^{\circ }$,$60^{\circ }$,$45^{\circ }$,$30^{\circ }$等特殊角时,常常想到把它们转化到特殊的三角形或特殊的四边形中。
【探究问题】由已知六边形各个内角为$120^{\circ }$,易得其内角的邻补角为$60^{\circ }$,从而联想到作其邻补角,得四边形,易证其为平行四边形,利用平行四边形的性质解决问题。于是,延长BA交EF的延长线于点M,延长BC交ED的延长线于点N。
$\because ∠1= ∠2= 120^{\circ }$,

$\therefore ∠3= ∠4= 60^{\circ }$,
$\therefore △MAF$是等边三角形。同理,$△NCD$也是等边三角形。
$\therefore ∠M= ∠N= 60^{\circ }$。
$\because ∠E= ∠B= 120^{\circ }$,
$\therefore ∠M+∠E= ∠M+∠B= 180^{\circ }$,
$\therefore ME// BN$,$MB// EN$,
$\therefore$四边形MBNE为平行四边形,
$\therefore ME= BN$。
$\because FA= FM$,$CD= CN$,
$\therefore EF+FA= BC+CD= 6$,
$\therefore AB+BC+CD+DE+EF+FA= 15$。
【方法归纳】将多边形的问题转化为三角形或四边形的问题不失为一种好方法,本例由题意知各角都为$120^{\circ }$,自然会联想到它的外角都为$60^{\circ }$,如延长各边,能得到等边三角形或平行四边形。当所遇问题中,涉及$120^{\circ }$,$60^{\circ }$,$45^{\circ }$,$30^{\circ }$等特殊角时,常常想到把它们转化到特殊的三角形或特殊的四边形中。
11.(★★★★☆)如图,在四边形ABCD中,$AB// CD$,$∠D= 2∠1$。若$AD= a$,$AB= b$,试求CD的长度。
思路点拨:过点B作$BE// AD$交DC的延长线于点E,构造平行四边形ABED。

解:过点B作$BE // AD$交DC的延长线于点E。
∵$AB // CD$,$BE // AD$,
∴四边形ABED是平行四边形,
∴$DE = AB = b$,$BE = AD = a$,$∠D = ∠E$。
∵$∠D = 2∠1$,
∴$∠E = 2∠1$。
∵$AB // CD$,
∴$∠1 = ∠BCE$。
在$\triangle BCE$中,$∠E = 2∠BCE$,
又∵$∠E + ∠BCE + ∠CBE = 180^\circ$,
且$∠CBE = 180^\circ - ∠E - ∠BCE = 180^\circ - 2∠BCE - ∠BCE = 180^\circ - 3∠BCE$,
又∵$BE // AD$,$AB // CD$,
∴$∠CBE = ∠1 = ∠BCE$(两直线平行,内错角相等),
∴$∠BCE = ∠CBE$,
∴$\triangle BCE$是等腰三角形,$CE = BE = a$。
∵$DE = CD + CE$,
∴$CD = DE - CE = b - a$。
答:$CD$的长度为
思路点拨:过点B作$BE// AD$交DC的延长线于点E,构造平行四边形ABED。

解:过点B作$BE // AD$交DC的延长线于点E。
∵$AB // CD$,$BE // AD$,
∴四边形ABED是平行四边形,
∴$DE = AB = b$,$BE = AD = a$,$∠D = ∠E$。
∵$∠D = 2∠1$,
∴$∠E = 2∠1$。
∵$AB // CD$,
∴$∠1 = ∠BCE$。
在$\triangle BCE$中,$∠E = 2∠BCE$,
又∵$∠E + ∠BCE + ∠CBE = 180^\circ$,
且$∠CBE = 180^\circ - ∠E - ∠BCE = 180^\circ - 2∠BCE - ∠BCE = 180^\circ - 3∠BCE$,
又∵$BE // AD$,$AB // CD$,
∴$∠CBE = ∠1 = ∠BCE$(两直线平行,内错角相等),
∴$∠BCE = ∠CBE$,
∴$\triangle BCE$是等腰三角形,$CE = BE = a$。
∵$DE = CD + CE$,
∴$CD = DE - CE = b - a$。
答:$CD$的长度为
$b - a$
。
答案:
解:过点B作$BE // AD$交DC的延长线于点E。
∵$AB // CD$,$BE // AD$,
∴四边形ABED是平行四边形,
∴$DE = AB = b$,$BE = AD = a$,$∠D = ∠E$。
∵$∠D = 2∠1$,
∴$∠E = 2∠1$。
∵$AB // CD$,
∴$∠1 = ∠BCE$。
在$\triangle BCE$中,$∠E = 2∠BCE$,
又
∵$∠E + ∠BCE + ∠CBE = 180^\circ$,
且$∠CBE = 180^\circ - ∠E - ∠BCE = 180^\circ - 2∠BCE - ∠BCE = 180^\circ - 3∠BCE$,
又
∵$BE // AD$,$AB // CD$,
∴$∠CBE = ∠1 = ∠BCE$(两直线平行,内错角相等),
∴$∠BCE = ∠CBE$,
∴$\triangle BCE$是等腰三角形,$CE = BE = a$。
∵$DE = CD + CE$,
∴$CD = DE - CE = b - a$。
答:$CD$的长度为$b - a$。
∵$AB // CD$,$BE // AD$,
∴四边形ABED是平行四边形,
∴$DE = AB = b$,$BE = AD = a$,$∠D = ∠E$。
∵$∠D = 2∠1$,
∴$∠E = 2∠1$。
∵$AB // CD$,
∴$∠1 = ∠BCE$。
在$\triangle BCE$中,$∠E = 2∠BCE$,
又
∵$∠E + ∠BCE + ∠CBE = 180^\circ$,
且$∠CBE = 180^\circ - ∠E - ∠BCE = 180^\circ - 2∠BCE - ∠BCE = 180^\circ - 3∠BCE$,
又
∵$BE // AD$,$AB // CD$,
∴$∠CBE = ∠1 = ∠BCE$(两直线平行,内错角相等),
∴$∠BCE = ∠CBE$,
∴$\triangle BCE$是等腰三角形,$CE = BE = a$。
∵$DE = CD + CE$,
∴$CD = DE - CE = b - a$。
答:$CD$的长度为$b - a$。
查看更多完整答案,请扫码查看


