《2025年七彩假日快乐假期暑假作业八年级数学》

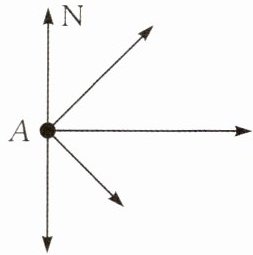
10.(★★☆☆☆)如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,两船相距(D)

A.25海里
B.30海里
C.35海里
D.40海里

答案： D

11.(★★☆☆☆)已知a,b,c分别为△ABC的三边长,且满足$(a^{2}-b^{2})(a^{2}+b^{2}-c^{2})= 0$,则它的形状为(D)
A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等腰三角形或直角三角形

答案： D

12.(★★☆☆☆)一个三角形的三边长分别为15cm,20cm,25cm,这个三角形最长边上的高是(D)
A.9cm
B.8cm
C.10cm
D.12cm

答案： D

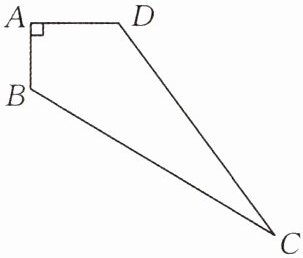
13.(★★★☆☆)如图,在四边形ABCD中,AB= 3cm,AD= 4cm,BC= 13cm,CD= 12cm,且∠A= 90°,求四边形ABCD的面积。

解：连接 $BD$。
$\because \angle A=90^{\circ}$，$\therefore BD=\sqrt{AB^{2}+AD^{2}}=$5。
又 $\because 5$，$12$，$13$ 是一组勾股数，$\therefore \triangle BCD$ 是直角三角形。$\therefore S_{四边形ABCD}=S_{\triangle ABD}+S_{\triangle BCD}=\frac{1}{2}× 3× 4+\frac{1}{2}× 5× 12=$36$(cm^{2})$。

答案： 解：连接 $BD$。
$\because \angle A=90^{\circ}$，$\therefore BD=\sqrt{AB^{2}+AD^{2}}=5$。
又 $\because 5$，$12$，$13$ 是一组勾股数，$\therefore \triangle BCD$ 是直角三角形。$\therefore S_{四边形ABCD}=S_{\triangle ABD}+S_{\triangle BCD}=\frac{1}{2}× 3× 4+\frac{1}{2}× 5× 12=36(cm^{2})$。

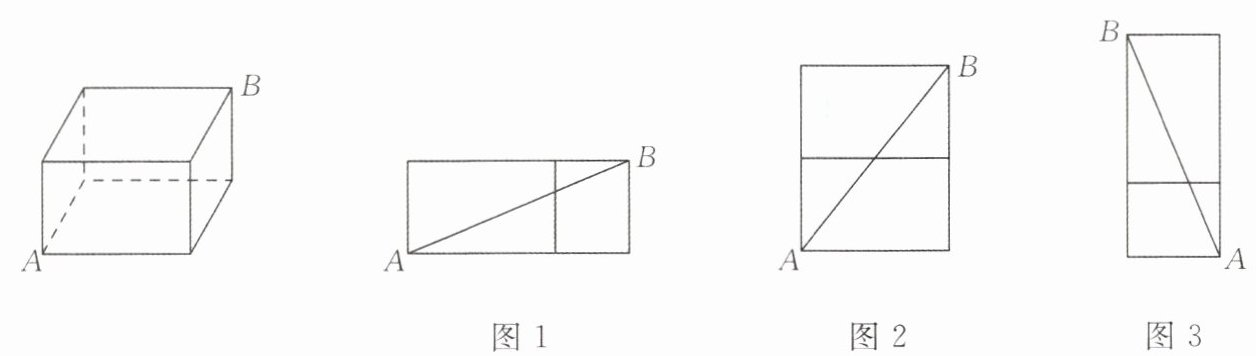
【提出问题】如图所示,长方体的长、宽、高分别是8cm,4cm,5cm,一只蚂蚁沿着长方体的表面从点A爬到点B,求蚂蚁爬行的最短路径长为$\sqrt{145}$cm。

答案： 【探究问题】解答此问题的关键是将立体图形展开成平面图形,利用平面几何的知识如对称、线段公理、点到直线的距离等求最短路径。因为长方体平面展开图不唯一,故应分情况分别计算,进行大小比较,再从各路线中确定最短的路线。长方体的平面展开图(部分)如上右边三个图形所示：
(1)如图1,展开前面、右面,由勾股定理得$AB^{2}= (8 + 4)^{2}+5^{2}= 169$；
(2)如图2,展开前面、上面,由勾股定理得$AB^{2}= (5 + 4)^{2}+8^{2}= 145$；
(3)如图3,展开左面、上面,由勾股定理得$AB^{2}= (8 + 5)^{2}+4^{2}= 185$。
∵$\sqrt{145}＜\sqrt{169}＜\sqrt{185}$,
∴最短路径长为$\sqrt{145}$cm。
【方法归纳】求立体图形上两点之间的距离时,应把它转化为平面图形来求解,“化曲面为平面”是解决“怎样爬行最短”这类问题的关键。解答这类问题时,要避免出现直接将两点连接,求线段长度的错误做法。