2025年七彩假日快乐假期暑假作业八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年七彩假日快乐假期暑假作业八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7.(★★☆☆☆)如图,已知某菱形花坛$ABCD$的周长是24 m,$∠BAD= 120^{\circ}$,则花坛对角线$AC$的长是(
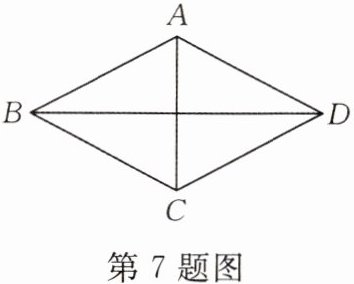
A.6$\sqrt{3}$m
B.6 m
C.3$\sqrt{3}$m
D.3 m
B
)
A.6$\sqrt{3}$m
B.6 m
C.3$\sqrt{3}$m
D.3 m
答案:
B
8.(★★☆☆☆)小明在学习了正方形之后,给同桌小文出了一道题,从下列四个条件“①$AB= BC$,②$∠ABC= 90^{\circ}$,③$AC= BD$,④$AC⊥BD$”中选两个作为补充条件,使$□ ABCD$成为正方形(如图).现有下列四种选法,你认为其中错误的是(
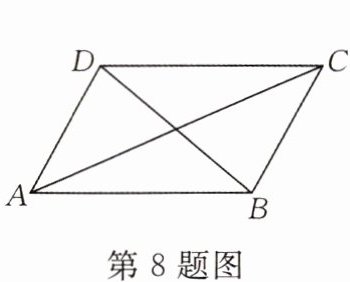
A.①②
B.②③
C.①③
D.②④
B
)
A.①②
B.②③
C.①③
D.②④
答案:
B
9.(★★★☆☆)如图,在菱形$ABCD$中,点$P是对角线AC$上一点,$PE⊥AB于点E$,若$PE= 3$,则点$P到AD$的距离为______
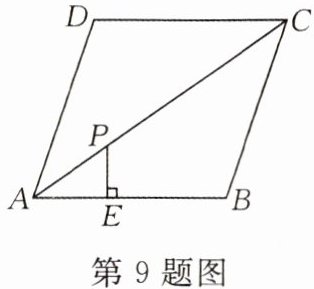
3
.
答案:
3
10.(★★★☆☆)如图,点$E在正方形ABCD的边CD$上,若$\triangle ABE$的面积为8,$CE= 3$,则线段$BE$的长为______
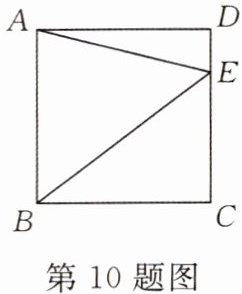
5
.
答案:
5
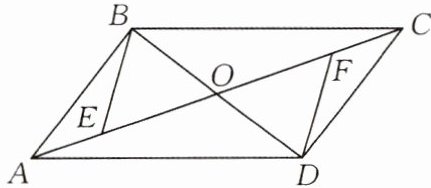
11.(★★★☆☆)如图,$□ ABCD的对角线AC$,$BD相交于点O$,$AE= CF$.
(1)求证:$\triangle BOE≌\triangle DOF$;
证明:∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC。
∵AE=CF,
∴OA-AE=OC-CF,即OE=OF。
在△BOE和△DOF中,
$\left\{\begin{array}{l} OB=OD,\\ ∠BOE=∠DOF,\\ OE=OF,\end{array}\right.$
∴△BOE≌△DOF(
(2)若$BD= EF$,连接$DE$,$BF$,判断四边形$EBFD$的形状,无须说明理由.
(1)求证:$\triangle BOE≌\triangle DOF$;
证明:∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC。
∵AE=CF,
∴OA-AE=OC-CF,即OE=OF。
在△BOE和△DOF中,
$\left\{\begin{array}{l} OB=OD,\\ ∠BOE=∠DOF,\\ OE=OF,\end{array}\right.$
∴△BOE≌△DOF(
SAS
)。(2)若$BD= EF$,连接$DE$,$BF$,判断四边形$EBFD$的形状,无须说明理由.
矩形

答案:
(1) 证明:
∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC。
∵AE=CF,
∴OA-AE=OC-CF,即OE=OF。
在△BOE和△DOF中,
$\left\{\begin{array}{l} OB=OD,\\ ∠BOE=∠DOF,\\ OE=OF,\end{array}\right.$
∴△BOE≌△DOF(SAS)。
(2) 矩形。
(1) 证明:
∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC。
∵AE=CF,
∴OA-AE=OC-CF,即OE=OF。
在△BOE和△DOF中,
$\left\{\begin{array}{l} OB=OD,\\ ∠BOE=∠DOF,\\ OE=OF,\end{array}\right.$
∴△BOE≌△DOF(SAS)。
(2) 矩形。
查看更多完整答案,请扫码查看


