《2025年七彩假日快乐假期暑假作业八年级数学》

处理中点 常想四法
【提出问题】如图,$∠ACB= 120^{\circ }$,以 AC,BC 为边长向外作正三角形 ACF,正三角形 BCE,点 P,M,N 分别为 AB,CF,CE 的中点.求证:PM= PN.
【探究问题】因为点 P,M,N 分别为 AB,CF,CE 的中点,所以我们可以利用 M,N 为等边三角形一边上的中点构造直角,然后利用点 P 为直角三角形斜边上的中点,证明 PM= PN.连接AM,BN.
$\because △ACF,△BCE$为等边三角形,$\therefore AF= AC,BC= BE.$
$\because M,N 分别为 CF,CE 的中点,\therefore AM⊥FC,BN⊥CE.$
又$\because P 为 AB 的中点,\therefore PM= \frac {1}{2}AB,PN= \frac {1}{2}AB.\therefore PM= PN.$
【方法归纳】遇到中点问题,常常有以下四种方法:①用连接法构造三角形的中位线(已知两中点,常连接另一点构造三角形的中位线);②用倍长法构造三角形的中位线(已知一中点,常倍长线段构造三角形的中位线);③取中点构造三角形中位线(已知一中点或两中点,常可另取中点构造三角形的中位线);④构造斜边上的中线(遇到直角三角形及斜边上的中点,考虑构造斜边上的中线).

答案： 【探究问题】因为点 P,M,N 分别为 AB,CF,CE 的中点,所以我们可以利用 M,N 为等边三角形一边上的中点构造直角,然后利用点 P 为直角三角形斜边上的中点,证明 PM= PN.连接 AM,BN.
$\because △ACF,△BCE$为等边三角形,$\therefore AF= AC,BC= BE.$
$\because M,N 分别为 CF,CE 的中点,\therefore AM⊥FC,BN⊥CE.$
又$\because P 为 AB 的中点,\therefore PM= \frac {1}{2}AB,PN= \frac {1}{2}AB.\therefore PM= PN.$
【方法归纳】遇到中点问题,常常有以下四种方法:①用连接法构造三角形的中位线(已知两中点,常连接另一点构造三角形的中位线);②用倍长法构造三角形的中位线(已知一中点,常倍长线段构造三角形的中位线);③取中点构造三角形中位线(已知一中点或两中点,常可另取中点构造三角形的中位线);④构造斜边上的中线(遇到直角三角形及斜边上的中点,考虑构造斜边上的中线).

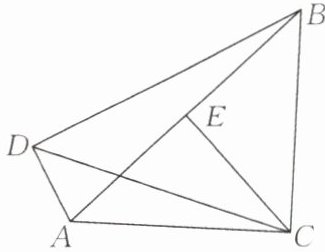
13.(★★★★☆)如图,在四边形 ACBD 中,$∠ACB= ∠ADB= 90^{\circ },∠DBC= 60^{\circ }$,E 是 AB 的中点.(1)求$∠DCE$的度数;30°(2)求$\frac {CE}{CD}$的值.$\frac{\sqrt{3}}{3}$
思路点拨:连接 DE,构造斜边上的中线.

答案：
(1)连接 DE。
∵∠ACB=∠ADB=90°，E 是 AB 中点，
∴CE=DE=AE=BE=1/2AB。
∵∠DBC=60°，
∴∠BCD=30°，∠CBD=60°。
∵CE=BE，DE=BE，
∴∠ECB=∠EBC，∠EDB=∠EBD。
设∠EBC=α，则∠ECB=α，∠EBD=60°-α，∠EDB=60°-α。
在△BCD 中，∠BDC=90°-∠BCD=60°，
∴∠EDC=∠BDC-∠EDB=60°-(60°-α)=α。
在△ECD 中，CE=DE，∠EDC=∠ECD=α，
又∠ACB=90°，∠ACB=∠ACE+∠ECB=∠ACE+α=90°，
∠ACE=∠ACD-∠ECD=∠ACD-α，
而∠ACD=∠ACB-∠BCD=90°-30°=60°，
∴60°-α+α=90°（矛盾，修正）：
∵∠DCE=∠ECB-∠BCD=α-30°，
∠EDC=∠EDB-∠CDB=(60°+α)-60°=α（∠EBD=∠EBC+∠CBD=α+60°），
在△ECD 中，∠DCE=∠EDC，即α-30°=α（错误），正确方法：
∵CE=DE=1/2AB，
∴C、D 在以 E 为圆心的圆上，
∠CED=2∠CBD=120°（同弧所对圆心角是圆周角 2 倍），
∴∠DCE=(180°-120°)/2=30°。
(2)过 E 作 EM⊥CD 于 M，
设 CE=DE=2x，在△CDE 中，∠DCE=30°，
EM=CE·sin30°=x，CM=CE·cos30°=√3x，
∵CE=DE，EM⊥CD，
∴CD=2CM=2√3x，
∴CE/CD=2x/(2√3x)=1/√3=√3/3。
答案：
(1)30°；
(2)√3/3。