《2025年七彩假日快乐假期暑假作业八年级数学》

10.(★★☆☆☆)直角三角形中一直角边的长为9,另两边长为连续自然数,则直角三角形的周长为(C)
A.121
B.120
C.90
D.不能确定

答案： C

11.(★★☆☆☆)如图,在$\triangle ABC$中,$∠C= 90^{\circ },BA= 15,AC= 12$,以直角边BC为直径作半圆,则这个半圆的面积是____10. 125π.

答案： 10. 125π

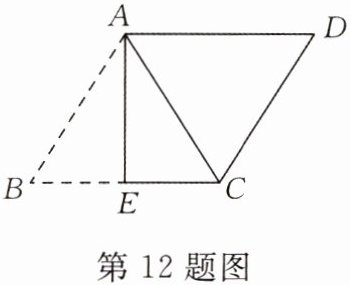
12.(★★☆☆☆)如图,在$□ ABCD$中,$AB= \sqrt {13},AD= 4$,将$□ ABCD$沿AE翻折后,点B恰好与点C重合,则折痕AE的长为____3.

答案： 3

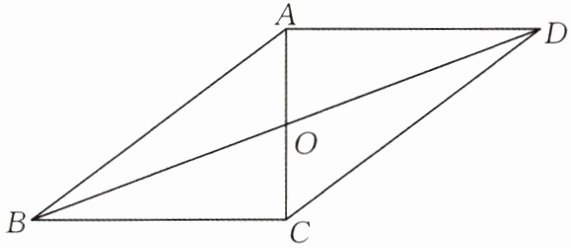
13.(★★★☆☆)如图,在$□ ABCD$中,AC,BD相交于点O,$AB= 10cm,AD= 8cm,AC⊥BC$,求OB的长.

解：
∵四边形ABCD是平行四边形，
∴BC=AD=8cm，OA=OC=1/2AC。
∵AC⊥BC，
∴∠ACB=90°。
在Rt△ABC中，AB=10cm，BC=8cm，
由勾股定理得：AC=√(AB²-BC²)=√(10²-8²)=6cm，
∴OC=1/2AC=3cm。
在Rt△OBC中，BC=8cm，OC=3cm，
由勾股定理得：OB=√(BC²+OC²)=√(8²+3²)=√73cm。
答：OB的长为√73cm。

答案： 解：
∵四边形ABCD是平行四边形，
∴BC=AD=8cm，OA=OC=1/2AC。
∵AC⊥BC，
∴∠ACB=90°。
在Rt△ABC中，AB=10cm，BC=8cm，
由勾股定理得：AC=√(AB²-BC²)=√(10²-8²)=6cm，
∴OC=1/2AC=3cm。
在Rt△OBC中，BC=8cm，OC=3cm，
由勾股定理得：OB=√(BC²+OC²)=√(8²+3²)=√73cm。
答：OB的长为√73cm。

“面积法”神通广大
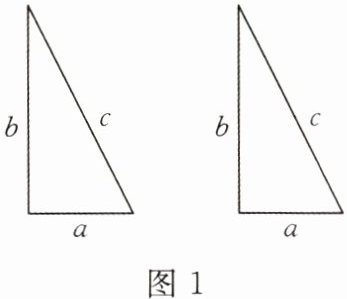
【提出问题】图1是用硬纸板做成的两个全等的直角三角形,两直角边长分别为a和b,斜边长为c;图2是以c为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个能证明勾股定理的图形.(1)画出拼成的图形的示意图,写出它的名称;(2)用这个图形证明勾股定理;(3)设图1中的直角三角形有若干个,你能运用图1中给的直角三角形拼出另外一种能证明勾股定理的图形吗?请画出拼成后的示意图.(无须证明)

答案：
【探究问题】小明是这样思考的:证明勾股定理采用的是面积法.因此,可以构造出我们熟悉的图形,并利用面积求证.小明的构造方法:利用两个如图1的直角三角形和一个如图2的直角三角形,构造一个直角梯形,根据面积相等可得$\frac {1}{2}(a+b)(a+b)= \frac {1}{2}ab×2+\frac {1}{2}c^{2}$,化简得$a^{2}+b^{2}= c^{2}$.
拼出的另外一种图形如下.

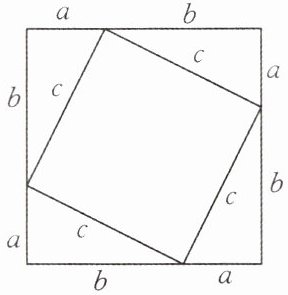
【方法归纳】我们把根据题目给出的条件,利用等积变换原理和有关计算面积的公式、定理或图形的面积关系进行解题的方法称为面积法.有些问题,从表面上看似乎与面积无关,但往往利用面积法求解,可以出奇制胜,做到事半功倍.等积法是利用面积法解题的常用方法和技巧.