2025年七彩假日快乐假期暑假作业八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年七彩假日快乐假期暑假作业八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
4.(★☆☆☆☆)已知a,b,c是三角形的三边长,如果满足$(a - 6)^{2}+\sqrt{b - 8}+|c - 10|= 0$,则这个三角形的形状是(
A.底与边不相等的等腰三角形
B.等边三角形
C.钝角三角形
D.直角三角形
D
)A.底与边不相等的等腰三角形
B.等边三角形
C.钝角三角形
D.直角三角形
答案:
D
5.(★★☆☆☆)等腰三角形的腰长为13,底边长为10,则顶角的平分线长为____
12
。
答案:
12
6.(★★☆☆☆)已知x,y为正数,且$|x^{2}-5|+(y^{2}-3)^{2}= 0$,如果以x、y的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为
8
。
答案:
8
7.(★★☆☆☆)如图,AD= 4,CD= 3,∠ADC= 90°,AB= 13,BC= 12,求该图形的面积。
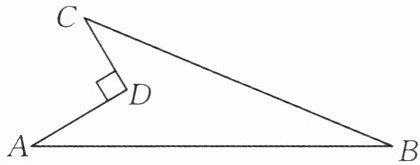
解:连接AC。
在Rt△ADC中,AD=4,CD=3,∠ADC=90°,
由勾股定理得:AC²=AD²+CD²=4²+3²=25,
∴AC=
在△ABC中,AC=5,BC=12,AB=13,
∵5²+12²=13²,即AC²+BC²=AB²,
∴△ABC是直角三角形,∠ACB=90°。
S△ADC=1/2×AD×CD=1/2×4×3=
S△ABC=1/2×AC×BC=1/2×5×12=
图形面积=S△ABC - S△ADC=30 - 6=
答:该图形的面积为24。

解:连接AC。
在Rt△ADC中,AD=4,CD=3,∠ADC=90°,
由勾股定理得:AC²=AD²+CD²=4²+3²=25,
∴AC=
5
。在△ABC中,AC=5,BC=12,AB=13,
∵5²+12²=13²,即AC²+BC²=AB²,
∴△ABC是直角三角形,∠ACB=90°。
S△ADC=1/2×AD×CD=1/2×4×3=
6
,S△ABC=1/2×AC×BC=1/2×5×12=
30
,图形面积=S△ABC - S△ADC=30 - 6=
24
。答:该图形的面积为24。
答案:
解:连接AC。
在Rt△ADC中,AD=4,CD=3,∠ADC=90°,
由勾股定理得:AC²=AD²+CD²=4²+3²=25,
∴AC=5。
在△ABC中,AC=5,BC=12,AB=13,
∵5²+12²=13²,即AC²+BC²=AB²,
∴△ABC是直角三角形,∠ACB=90°。
S△ADC=1/2×AD×CD=1/2×4×3=6,
S△ABC=1/2×AC×BC=1/2×5×12=30,
图形面积=S△ABC - S△ADC=30 - 6=24。
答:该图形的面积为24。
在Rt△ADC中,AD=4,CD=3,∠ADC=90°,
由勾股定理得:AC²=AD²+CD²=4²+3²=25,
∴AC=5。
在△ABC中,AC=5,BC=12,AB=13,
∵5²+12²=13²,即AC²+BC²=AB²,
∴△ABC是直角三角形,∠ACB=90°。
S△ADC=1/2×AD×CD=1/2×4×3=6,
S△ABC=1/2×AC×BC=1/2×5×12=30,
图形面积=S△ABC - S△ADC=30 - 6=24。
答:该图形的面积为24。
8.(★★☆☆☆)如图,正方形网格中的△ABC,若小方格边长为1,试证明△ABC是直角三角形。
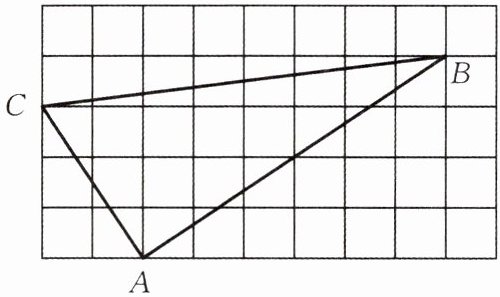
证明:由图可知,小方格边长为1。
$AC^2 = 2^2 + 3^2 = 4 + 9 = 13$,
$AB^2 = 6^2 + 4^2 = 36 + 16 = 52$,
$BC^2 = 8^2 + 1^2 = 64 + 1 = 65$。
$\because 13 + 52 = 65$,
$\therefore AC^2 + AB^2 = BC^2$。
$\therefore \angle CAB = 90^\circ$。
$\therefore \triangle ABC$是直角三角形。

证明:由图可知,小方格边长为1。
$AC^2 = 2^2 + 3^2 = 4 + 9 = 13$,
$AB^2 = 6^2 + 4^2 = 36 + 16 = 52$,
$BC^2 = 8^2 + 1^2 = 64 + 1 = 65$。
$\because 13 + 52 = 65$,
$\therefore AC^2 + AB^2 = BC^2$。
$\therefore \angle CAB = 90^\circ$。
$\therefore \triangle ABC$是直角三角形。
答案:
证明:由图可知,小方格边长为1。
$AC^2 = 2^2 + 3^2 = 4 + 9 = 13$,
$AB^2 = 6^2 + 4^2 = 36 + 16 = 52$,
$BC^2 = 8^2 + 1^2 = 64 + 1 = 65$。
$\because 13 + 52 = 65$,
$\therefore AC^2 + AB^2 = BC^2$。
$\therefore \angle CAB = 90^\circ$。
$\therefore \triangle ABC$是直角三角形。
$AC^2 = 2^2 + 3^2 = 4 + 9 = 13$,
$AB^2 = 6^2 + 4^2 = 36 + 16 = 52$,
$BC^2 = 8^2 + 1^2 = 64 + 1 = 65$。
$\because 13 + 52 = 65$,
$\therefore AC^2 + AB^2 = BC^2$。
$\therefore \angle CAB = 90^\circ$。
$\therefore \triangle ABC$是直角三角形。
9.(★★☆☆☆)如图,在长方形ABCD中,AB= 3cm,AD= 9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为(
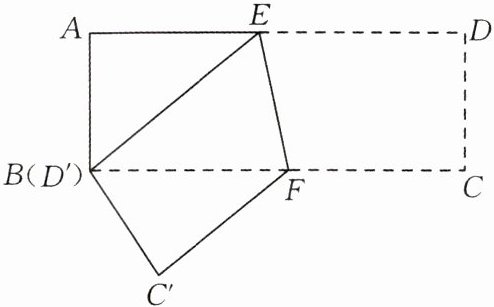
A.$6cm^{2}$
B.$8cm^{2}$
C.$10cm^{2}$
D.$12cm^{2}$
A
)
A.$6cm^{2}$
B.$8cm^{2}$
C.$10cm^{2}$
D.$12cm^{2}$
答案:
A
查看更多完整答案,请扫码查看


