《2025年七彩假日快乐假期暑假作业八年级数学》

2.如图1,将三角板放在正方形$ABCD$上,使三角板的直角顶点$E与正方形ABCD的顶点A$重合,三角板的一边交$CD于点F$,另一边交$CB的延长线于点G$.


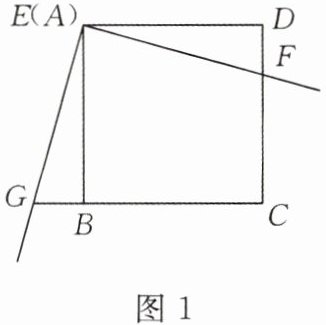
(1)求证:$EF= EG$;
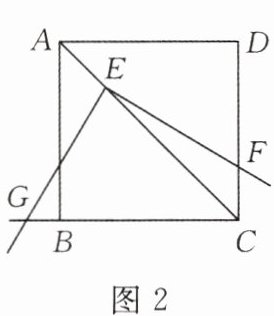
(2)如图2,移动三角板,使顶点$E始终在正方形ABCD的对角线AC$上,其他条件不变.(1)中的结论是否仍然成立? 若成立,请给予证明;若不成立,请说明理由.
思路点拨:第(1)小题可以通过直接证明$\triangle EDF≌\triangle EBG$来求证;第(2)小题是动态画图题,其证明的思路与第(1)小题类似.

答案：

(1) 证明: $ \because \angle DEF + \angle BEF = 90 ^ { \circ }, \angle GEB + $ $ \angle B E F = 90 ^ { \circ }, \therefore \angle D E F = \angle G E B $.
又 $ \because E D = E B, \therefore \mathrm { Rt } \triangle E F D \cong \mathrm { Rt } \triangle E G B $ (ASA). $ \therefore E F = E G $;
(2) 解: 成立. 证明如下: 如图, 过点 E 分别作 BC, CD 的垂线, 垂足分别为 H, I, 则 $ E H = E I $, $ \angle H E I = 90 ^ { \circ }. \because \angle I E F + \angle H E F = 90 ^ { \circ }, \angle G E H $ $ + \angle H E F = 90 ^ { \circ }, \therefore \angle I E F = \angle G E H $, $ \therefore \mathrm { Rt } \triangle F E I \cong \mathrm { Rt } \triangle G E H ( \mathrm { ASA } ), \therefore E F = E G $.

3.如图,在等边三角形$ABC$中,$BC= 6$cm,射线$AG// BC$,点$E从点A出发沿射线AG$以1 cm/s的速度运动,同时点$F从点B出发沿射线BC$以2 cm/s的速度运动,设运动时间为$t$(单位:s).
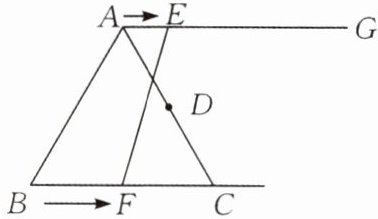
(1)连接$EF$,当$EF经过AC边的中点D$时,求证:$\triangle ADE≌\triangle CDF$;
(2)当$t$为多少秒时,四边形$ACFE$为菱形?6
思路点拨:第(1)小题可以直接运用“AAS”证明$\triangle ADE≌\triangle CDF$;第(2)小题是运动型问题,假设四边形$ACFE$是菱形,则有$AE= AC= CF= EF$,即可构建关于$t$的方程从而求解.

答案：
(1) 证明：因为 $AG // BC$，所以 $\angle EAD = \angle FCD$，$\angle AED = \angle CFD$。
又因为 $D$ 是 $AC$ 的中点，所以 $AD = CD$。
在 $\triangle ADE$ 和 $\triangle CDF$ 中，
$\begin{cases}\angle EAD = \angle FCD \\\angle AED = \angle CFD \\AD = CD\end{cases}$
所以 $\triangle ADE \cong \triangle CDF$（AAS）。
(2) 解：当四边形 $ACFE$ 是菱形时，$AE = AC = CF$。
因为 $\triangle ABC$ 是等边三角形，所以 $AC = BC = 6\ \text{cm}$，即 $AE = 6\ \text{cm}$。
由题意得 $AE = t$，所以 $t = 6$。
此时 $CF = 2t - 6 = 2 × 6 - 6 = 6\ \text{cm}$，满足 $CF = AC$。
故当 $t = 6\ \text{s}$ 时，四边形 $ACFE$ 为菱形。
答案：
(2) $6\ \text{s}$