《2025年综合应用创新题典中点六年级数学上册人教版》

1. 荣德小学组织六年级同学进行包饺子比赛,在同样多的时间内,获得冠军的典典包了60个,比获得亚军的梦梦多包了$\frac{1}{4}$,梦梦又比获得季军的华华多包了$\frac{1}{5}$。
(1)获得亚军的梦梦包了多少个饺子？(先写出等量关系式,再列方程解答)
(2)获得季军的华华包了多少个饺子？(先列方程解答,再用算术方法解答)

答案： 1.（1）梦梦包的个数×$(1+\frac{1}{4})=$典典包的个数
解：设获得亚军的梦梦包了x个饺子。
$(1+\frac{1}{4})x=60$
$x=48$ 答：获得亚军的梦梦包了48个饺子。
【点拨】根据题意可列出等量关系式：梦梦包的个数×$(1+\frac{1}{4})=$典典包的个数。设获得亚军的梦梦包了x个饺子，根据等量关系式列方程解答。
（2）解：设获得季军的华华包了x个饺子。
$(1+\frac{1}{5})x=48$
$x=40$
$48÷(1+\frac{1}{5})=40$（个）
答：获得季军的华华包了40个饺子。
【点拨】根据题意可列出等量关系式：华华包的个数×$(1+\frac{1}{5})=$梦梦包的个数。设获得季军的华华包了x个饺子，根据等量关系式列方程解答。也可直接用除法求出华华包了多少个饺子。

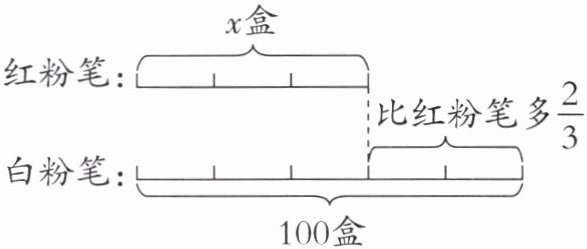
2. 看图列方程解答。

答案： 2.$(1+\frac{2}{3})x=100$
解：$x=60$

3. 中岳嵩山海拔约1500 m,比西岳华山的海拔低了约$\frac{7}{22}$,西岳华山海拔约多少米？(列方程解答)

答案： 3. 解：设西岳华山海拔约x m。
$(1-\frac{7}{22})x=1500$
$x=2200$ 答：西岳华山海拔约2200 m。
【点拨】根据题意可列出等量关系式：西岳华山的海拔×$(1-\frac{7}{22})=$中岳嵩山的海拔。设西岳华山海拔约x m，根据等量关系式列方程解答。

4. 实验小学这学期校本课程中新增了轮滑课程和沙画课程。参加轮滑课程的有72人,比参加沙画课程的人数少$\frac{1}{5}$,参加沙画课程的有多少人？(提出一个用两步或两步以上计算解决的问题并解答)
$72÷(1-\frac{1}{5})=90$（人） 答：参加沙画课程的有90人。

答案： 4.（答案不唯一）参加沙画课程的有多少人
$72÷(1-\frac{1}{5})=90$（人） 答：参加沙画课程的有90人。
【点拨】必须提出一个用两步或两步以上计算解决的问题，答案合理即可。

5. 北京烤鸭是北京特色美食,又称烤填鸭,肉质细嫩丰腴。一家饭店今天售出了烤鸭60只,比昨天多$\frac{1}{5}$,今天比昨天多售出多少只？
提示：今天比昨天多售出的部分是昨天的$\frac{1}{5}$。

答案： 5.$60÷(1+\frac{1}{5})×\frac{1}{5}=10$（只） 答：今天比昨天多售出10只。
【点拨】已知比一个数多几分之几的数是多少，求这个数，用除法计算，据此求出昨天售出的只数，再乘$\frac{1}{5}$即可求出今天比昨天多售出的只数。

6. 华华上周弄丢了一些“天天向上”的积分卡,只剩下原来积分卡张数的$\frac{4}{5}$。这一周华华各方面表现优异,老师奖励了她7张积分卡,现在积分卡的张数比原来多$\frac{4}{15}$。华华现在一共有多少张积分卡？(列方程解答)

答案： 6. 解：设华华原来有x张积分卡。
$\frac{4}{5}x+7=(1+\frac{4}{15})x$
$x=15$ $15×(1+\frac{4}{15})=19$（张）
答：华华现在一共有19张积分卡。
【点拨】根据题意可列出等量关系式：华华剩下的积分卡的张数$+7=$华华原来的积分卡的张数×$(1+\frac{4}{15})$。设华华原来有x张积分卡，根据等量关系式列方程解答，求出华华原来的积分卡张数，进而求出华华现在一共有的积分卡的张数。