第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
(1)计算$\frac{5}{12}+\frac{7}{12}×\frac{4}{21}$时,先算
乘
法,再算加
法,结果是$\frac{19}{36}$
。
答案:
解析:本题考查了四则运算的运算顺序,在含有两级的运算中,要先算乘除,后算加减。有括号的先算括号里面的。本题没有括号,先算乘法$\frac{7}{12}×\frac{4}{21}=\frac{1}{9}$,再算加法$\frac{5}{12}+\frac{1}{9}=\frac{19}{36}$。
答案:$\frac{5}{12}+\frac{7}{12}×\frac{4}{21}$
$=\frac{5}{12}+\frac{1}{9}$
$=\frac{15}{36}+\frac{4}{36}$
$=\frac{19}{36}$
答案:$\frac{5}{12}+\frac{7}{12}×\frac{4}{21}$
$=\frac{5}{12}+\frac{1}{9}$
$=\frac{15}{36}+\frac{4}{36}$
$=\frac{19}{36}$
(2)在〇里填上“>”“<”或“=”。
$\frac{7}{9}×\frac{4}{5}×\frac{2}{3}$〇
$\frac{1}{2}+\frac{5}{4}×\frac{1}{2}$〇
$(1-\frac{2}{7})×\frac{1}{5}$〇
$\frac{7}{9}×\frac{4}{5}×\frac{2}{3}$〇
<
$\frac{7}{9}$$\frac{1}{2}+\frac{5}{4}×\frac{1}{2}$〇
>
$(\frac{1}{2}+\frac{5}{4})×\frac{1}{2}$$(1-\frac{2}{7})×\frac{1}{5}$〇
<
$1-\frac{2}{7}×\frac{1}{5}$
答案:
解析:
第一组:
题目考查的是分数乘法与比较大小。
当一个数(大于0)乘以一个比1小的数时,结果会比原数小。
因为$\frac{4}{5} \lt 1$且$\frac{2}{3} \lt 1$,
所以$\frac{7}{9} × \frac{4}{5} × \frac{2}{3} \lt \frac{7}{9}$。
第二组:
题目考查的是分数四则运算的顺序和分配律。
需要先分别计算两边的结果,再比较大小。
左边可以先把公因数$\frac{1}{2}$提出来,得到$\frac{1}{2} × (1+\frac{5}{4} )=\frac{9}{8} $,
而右边为$(\frac{1}{2}+\frac{5}{4})×\frac{1}{2}=\frac{7}{4} × \frac{1}{2}=\frac{7}{8} $,
所以$\frac{1}{2}+\frac{5}{4}×\frac{1}{2} \gt (\frac{1}{2}+\frac{5}{4})×\frac{1}{2}$。
第三组:
题目考查分数四则运算的顺序。
按照运算顺序,先算括号里的,再进行乘法或减法运算,最后比较结果。
左边为$(1-\frac{2}{7})×\frac{1}{5}=1× \frac{1}{5}-\frac{2}{7}× \frac{1}{5}=\frac{1}{5}-\frac{2}{35}=\frac{1}{7}$,
而右边为$1-\frac{2}{7}×\frac{1}{5}=\frac{33}{35}$,
所以$(1-\frac{2}{7})×\frac{1}{5} \lt 1-\frac{2}{7}×\frac{1}{5}$。
答案:
<;>;<
第一组:
题目考查的是分数乘法与比较大小。
当一个数(大于0)乘以一个比1小的数时,结果会比原数小。
因为$\frac{4}{5} \lt 1$且$\frac{2}{3} \lt 1$,
所以$\frac{7}{9} × \frac{4}{5} × \frac{2}{3} \lt \frac{7}{9}$。
第二组:
题目考查的是分数四则运算的顺序和分配律。
需要先分别计算两边的结果,再比较大小。
左边可以先把公因数$\frac{1}{2}$提出来,得到$\frac{1}{2} × (1+\frac{5}{4} )=\frac{9}{8} $,
而右边为$(\frac{1}{2}+\frac{5}{4})×\frac{1}{2}=\frac{7}{4} × \frac{1}{2}=\frac{7}{8} $,
所以$\frac{1}{2}+\frac{5}{4}×\frac{1}{2} \gt (\frac{1}{2}+\frac{5}{4})×\frac{1}{2}$。
第三组:
题目考查分数四则运算的顺序。
按照运算顺序,先算括号里的,再进行乘法或减法运算,最后比较结果。
左边为$(1-\frac{2}{7})×\frac{1}{5}=1× \frac{1}{5}-\frac{2}{7}× \frac{1}{5}=\frac{1}{5}-\frac{2}{35}=\frac{1}{7}$,
而右边为$1-\frac{2}{7}×\frac{1}{5}=\frac{33}{35}$,
所以$(1-\frac{2}{7})×\frac{1}{5} \lt 1-\frac{2}{7}×\frac{1}{5}$。
答案:
<;>;<
(3)$42×(\frac{13}{14}-\frac{8}{21})=$
42
×$\frac{13}{14}$
-
42
×$\frac{8}{21}$
,这里运用了(乘法分配)律。
答案:
解析:题目考查乘法分配律,即$a×(b - c)=a× b - a× c$。对于$42×(\frac{13}{14}-\frac{8}{21})$,根据乘法分配律可得$42×\frac{13}{14}-42×\frac{8}{21}$。
答案:$42$;$\frac{13}{14}$;$-$;$42$;$\frac{8}{21}$
答案:$42$;$\frac{13}{14}$;$-$;$42$;$\frac{8}{21}$
(4)新考法 分析法 《水浒传》是中国历史上第一部以白话文写成的章回体长篇小说。蓝蓝买了一本 752 页的《水浒传》,第一周读了全书的$\frac{1}{8}$,第二周读的页数是第一周的$\frac{1}{2}$。$752×\frac{1}{8}×\frac{1}{2}$的运算结果表示
第二周读的页数
,$\frac{1}{8}×\frac{1}{2}= \frac{1}{16}$,这里的$\frac{1}{16}$表示的意思是第二周读的页数占全书的几分之几
。
答案:
解析:
题目考查分数乘法的意义,通过分析题目中的数量关系,理解分数乘法在实际问题中的应用。
第一问:根据已知条件,全书共$752$页,第一周读了全书的$\frac{1}{8}$,第二周读的页数是第一周的$\frac{1}{2}$,所以$752×\frac{1}{8}×\frac{1}{2}$表示第二周读的页数。
第二问:把全书页数看作单位“$1$”,第一周读了全书的$\frac{1}{8}$,第二周读的页数是第一周的$\frac{1}{2}$,那么$\frac{1}{8}×\frac{1}{2}=\frac{1}{16}$,表示第二周读的页数占全书的$\frac{1}{16}$。
答案:
第二周读的页数;第二周读的页数占全书的几分之几。
题目考查分数乘法的意义,通过分析题目中的数量关系,理解分数乘法在实际问题中的应用。
第一问:根据已知条件,全书共$752$页,第一周读了全书的$\frac{1}{8}$,第二周读的页数是第一周的$\frac{1}{2}$,所以$752×\frac{1}{8}×\frac{1}{2}$表示第二周读的页数。
第二问:把全书页数看作单位“$1$”,第一周读了全书的$\frac{1}{8}$,第二周读的页数是第一周的$\frac{1}{2}$,那么$\frac{1}{8}×\frac{1}{2}=\frac{1}{16}$,表示第二周读的页数占全书的$\frac{1}{16}$。
答案:
第二周读的页数;第二周读的页数占全书的几分之几。
(5)比 25 m 长$\frac{1}{5}$是(30)m,比 25 m 短$\frac{1}{5}$是(20)m。甲绳长$\frac{4}{5}$m,乙绳比甲绳长$\frac{1}{4}$,乙绳长(1)m。
答案:
比25m长$\frac{1}{5}$:$25 + 25×\frac{1}{5} = 25 + 5 = 30$(m)
比25m短$\frac{1}{5}$:$25 - 25×\frac{1}{5} = 25 - 5 = 20$(m)
乙绳长:$\frac{4}{5} + \frac{4}{5}×\frac{1}{4} = \frac{4}{5} + \frac{1}{5} = 1$(m)
答案依次为:30;20;1
比25m短$\frac{1}{5}$:$25 - 25×\frac{1}{5} = 25 - 5 = 20$(m)
乙绳长:$\frac{4}{5} + \frac{4}{5}×\frac{1}{4} = \frac{4}{5} + \frac{1}{5} = 1$(m)
答案依次为:30;20;1
(6)六(1)班开展“捡拾白色垃圾,共创美丽家园”的环保活动。蓝蓝每天清理白色垃圾$\frac{5}{6}$kg,华华每天清理白色垃圾$\frac{3}{4}$kg,她们 12 天共清理白色垃圾(19)kg。
$\frac{5}{6} × 12 + \frac{3}{4} × 12$
$=10 + 9$
$=19$(kg)
答:她们12天共清理白色垃圾19kg。
$\frac{5}{6} × 12 + \frac{3}{4} × 12$
$=10 + 9$
$=19$(kg)
答:她们12天共清理白色垃圾19kg。
答案:
$\frac{5}{6} × 12 + \frac{3}{4} × 12$
$=10 + 9$
$=19$(kg)
答:她们12天共清理白色垃圾19kg。
$=10 + 9$
$=19$(kg)
答:她们12天共清理白色垃圾19kg。
(7)两根长$\frac{4}{5}$m 的铁丝,第一根截去$\frac{1}{4}$m,还剩(
$\frac{11}{20}$
)m;第二根截去全长的$\frac{1}{4}$,还剩下($\frac{3}{5}$
)m。
答案:
解析:
第一根铁丝的问题相对简单,直接用总长减去截去的长度即可。
对于第二根铁丝,需要理解“截去全长的$\frac{1}{4}$”这一表述。这意味着铁丝剩下的长度是原长度的$\frac{3}{4}$。
因此,我们只需要将原长度$\frac{4}{5}$乘以$\frac{3}{4}$即可求出剩下的长度。
答案:
第一根铁丝剩下的长度:
$\frac{4}{5} - \frac{1}{4} = \frac{16}{20} - \frac{5}{20} = \frac{11}{20} \text{(m)}$,
第二根铁丝剩下的长度:
$\frac{4}{5} × \left(1 - \frac{1}{4}\right) = \frac{4}{5} × \frac{3}{4} = \frac{3}{5} \text{(m)}$,
所以,第一根铁丝剩下$\frac{11}{20}$m,第二根铁丝剩下$\frac{3}{5}$m。
第一根铁丝的问题相对简单,直接用总长减去截去的长度即可。
对于第二根铁丝,需要理解“截去全长的$\frac{1}{4}$”这一表述。这意味着铁丝剩下的长度是原长度的$\frac{3}{4}$。
因此,我们只需要将原长度$\frac{4}{5}$乘以$\frac{3}{4}$即可求出剩下的长度。
答案:
第一根铁丝剩下的长度:
$\frac{4}{5} - \frac{1}{4} = \frac{16}{20} - \frac{5}{20} = \frac{11}{20} \text{(m)}$,
第二根铁丝剩下的长度:
$\frac{4}{5} × \left(1 - \frac{1}{4}\right) = \frac{4}{5} × \frac{3}{4} = \frac{3}{5} \text{(m)}$,
所以,第一根铁丝剩下$\frac{11}{20}$m,第二根铁丝剩下$\frac{3}{5}$m。
(8)新题型 数学文化题 《九章算术》约成书于东汉之初,共收有 246 个数学问题。杨老师利用暑假研究了其中的$\frac{1}{6}$,还剩下(
$\frac{5}{6}$
),还剩下(205
)个数学问题没有研究。
答案:
1. $1-\frac{1}{6}=\frac{5}{6}$
2. $246×\frac{5}{6}=205$(个)
还剩下$\frac{5}{6}$,还剩下205个数学问题没有研究。
2. $246×\frac{5}{6}=205$(个)
还剩下$\frac{5}{6}$,还剩下205个数学问题没有研究。
(1)新考法 数形结合法 图形  描述的数量关系是
描述的数量关系是
A.$9×\frac{1}{3}×2$
B.$9×\frac{2}{9}+\frac{2}{3}$
C.$9×\frac{1}{3}×\frac{2}{3}$
D.$3×\frac{1}{3}×\frac{2}{3}$
 描述的数量关系是
描述的数量关系是C
。A.$9×\frac{1}{3}×2$
B.$9×\frac{2}{9}+\frac{2}{3}$
C.$9×\frac{1}{3}×\frac{2}{3}$
D.$3×\frac{1}{3}×\frac{2}{3}$
答案:
解析:本题可根据图形所表示的数量关系,结合分数乘法的意义来进行分析。
从图形中可以看出,先把$9$平均分成$3$份,取其中的$1$份,即$9×\frac{1}{3}$;然后再把所得的结果平均分成$3$份,取其中的$2$份,也就是在$9×\frac{1}{3}$的基础上再乘$\frac{2}{3}$,所以整个图形描述的数量关系是$9×\frac{1}{3}×\frac{2}{3}$。
答案:C。
从图形中可以看出,先把$9$平均分成$3$份,取其中的$1$份,即$9×\frac{1}{3}$;然后再把所得的结果平均分成$3$份,取其中的$2$份,也就是在$9×\frac{1}{3}$的基础上再乘$\frac{2}{3}$,所以整个图形描述的数量关系是$9×\frac{1}{3}×\frac{2}{3}$。
答案:C。
一辆客车从武汉开往南京,到合肥站时,车上人数的$\frac{1}{6}$下车,然后上来车上现有人数的$\frac{1}{6}$,这时车上人数
A.和原来一样多
B.比原来多
C.比原来少
D.无法确定
C
。A.和原来一样多
B.比原来多
C.比原来少
D.无法确定
答案:
解析:本题考查分数应用题。
设客车原来的人数为$x$人。
到合肥站时,下车的人数是车上人数的$\frac{1}{6}$,即下车$\frac{1}{6}x$人,此时车上剩下的人数为$x-\frac{1}{6}x=\frac{5}{6}x$(人)。
然后上来车上现有人数的$\frac{1}{6}$,即上来$\frac{5}{6}x × \frac{1}{6}=\frac{5}{36}x$(人),此时车上的人数变为$\frac{5}{6}x+\frac{5}{36}x=\frac{30}{36}x+\frac{5}{36}x=\frac{35}{36}x$(人)。
因为$\frac{35}{36}x \lt x$,所以这时车上的人数比原来少。
答案:C。
设客车原来的人数为$x$人。
到合肥站时,下车的人数是车上人数的$\frac{1}{6}$,即下车$\frac{1}{6}x$人,此时车上剩下的人数为$x-\frac{1}{6}x=\frac{5}{6}x$(人)。
然后上来车上现有人数的$\frac{1}{6}$,即上来$\frac{5}{6}x × \frac{1}{6}=\frac{5}{36}x$(人),此时车上的人数变为$\frac{5}{6}x+\frac{5}{36}x=\frac{30}{36}x+\frac{5}{36}x=\frac{35}{36}x$(人)。
因为$\frac{35}{36}x \lt x$,所以这时车上的人数比原来少。
答案:C。
(3)一个长方形劳动基地,长 18 m,宽是长的$\frac{5}{9}$,它的面积是多少?列式正确的是
A.$18×\frac{5}{9}$
B.$18×\frac{5}{9}+18$
C.$18×\frac{5}{9}×18$
D.$(18×\frac{5}{9}+18)×2$
C
。A.$18×\frac{5}{9}$
B.$18×\frac{5}{9}+18$
C.$18×\frac{5}{9}×18$
D.$(18×\frac{5}{9}+18)×2$
答案:
解析:本题主要考察长方形面积的计算。
首先,需要找出长方形的长和宽,题目已经给出长是18m,宽是长的$\frac{5}{9}$,所以可以通过计算找出宽的长度,即:$宽 = 18 × \frac{5}{9} = 10m$。
然后,根据长方形面积的计算公式:$面积 = 长 × 宽$,可以计算出长方形的面积,即:$面积 = 18 × 10 = 180 m^{2}$。
所以,列式正确的是$18 × \frac{5}{9} × 18$,对应选项C。
答案:C。
首先,需要找出长方形的长和宽,题目已经给出长是18m,宽是长的$\frac{5}{9}$,所以可以通过计算找出宽的长度,即:$宽 = 18 × \frac{5}{9} = 10m$。
然后,根据长方形面积的计算公式:$面积 = 长 × 宽$,可以计算出长方形的面积,即:$面积 = 18 × 10 = 180 m^{2}$。
所以,列式正确的是$18 × \frac{5}{9} × 18$,对应选项C。
答案:C。
(4)新考法 图示信息法 图书角有三种图书,数量情况如下图。用“$300×(\frac{2}{5}-\frac{1}{3})$”可以求出
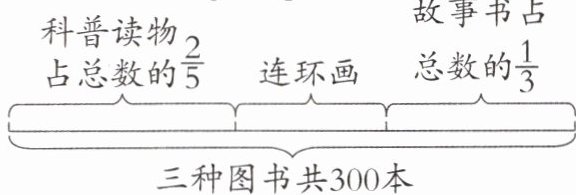
A.科普读物的本数
B.科普读物与故事书相差的本数
C.科普读物和故事书的总本数
D.连环画的本数
B
。
A.科普读物的本数
B.科普读物与故事书相差的本数
C.科普读物和故事书的总本数
D.连环画的本数
答案:
解析:
本题可根据所给算式$300×(\frac{2}{5} - \frac{1}{3})$,结合题目中三种图书数量与总数的关系来分析其意义。
步骤一:分析算式中各部分的含义
已知三种图书共$300$本,$\frac{2}{5}$是科普读物占总数的比例,$\frac{1}{3}$是故事书占总数的比例。
步骤二:分析$(\frac{2}{5} - \frac{1}{3})$的意义
$\frac{2}{5} - \frac{1}{3}$表示科普读物占总数的比例与故事书占总数的比例之差。
步骤三:分析$300×(\frac{2}{5} - \frac{1}{3})$的意义
根据求一个数的几分之几是多少用乘法计算,$300×(\frac{2}{5} - \frac{1}{3})$表示的就是科普读物比故事书多的数量占总数$300$本的部分,即科普读物与故事书相差的本数。
答案:B。
本题可根据所给算式$300×(\frac{2}{5} - \frac{1}{3})$,结合题目中三种图书数量与总数的关系来分析其意义。
步骤一:分析算式中各部分的含义
已知三种图书共$300$本,$\frac{2}{5}$是科普读物占总数的比例,$\frac{1}{3}$是故事书占总数的比例。
步骤二:分析$(\frac{2}{5} - \frac{1}{3})$的意义
$\frac{2}{5} - \frac{1}{3}$表示科普读物占总数的比例与故事书占总数的比例之差。
步骤三:分析$300×(\frac{2}{5} - \frac{1}{3})$的意义
根据求一个数的几分之几是多少用乘法计算,$300×(\frac{2}{5} - \frac{1}{3})$表示的就是科普读物比故事书多的数量占总数$300$本的部分,即科普读物与故事书相差的本数。
答案:B。
(5)新角度 补充条件 零食店有 8 kg 杏仁,______,还剩多少千克?请你根据算式$(8-\frac{3}{5})×(1-\frac{3}{5})$补充横线上的条件是
A.顾客甲买了$\frac{3}{5}$kg,顾客乙买了$\frac{3}{5}$kg
B.顾客甲买了$\frac{3}{5}$,顾客乙买了剩下的$\frac{3}{5}$
C.顾客甲买了$\frac{3}{5}$,顾客乙买了剩下的$\frac{3}{5}$kg
D.顾客甲买了$\frac{3}{5}$kg,顾客乙买了剩下的$\frac{3}{5}$
D
。A.顾客甲买了$\frac{3}{5}$kg,顾客乙买了$\frac{3}{5}$kg
B.顾客甲买了$\frac{3}{5}$,顾客乙买了剩下的$\frac{3}{5}$
C.顾客甲买了$\frac{3}{5}$,顾客乙买了剩下的$\frac{3}{5}$kg
D.顾客甲买了$\frac{3}{5}$kg,顾客乙买了剩下的$\frac{3}{5}$
答案:
解析:
本题考查的是分数的应用。
题目给出了一个算式 $(8-\frac{3}{5})×(1-\frac{3}{5})$,需要根据这个算式来补充横线上的条件。
首先,看到算式中有两个因子:$(8-\frac{3}{5})$ 和 $(1-\frac{3}{5})$。
第一个因子 $(8-\frac{3}{5})$ 表示原始数量 8 kg 减去一个确定的量 $\frac{3}{5}$ kg,这可以理解为顾客甲购买的数量。
第二个因子 $(1-\frac{3}{5})$ 表示剩余数量(即 $8-\frac{3}{5}$)再减去剩余数量的 $\frac{3}{5}$,这可以理解为顾客乙购买的数量是剩余数量的 $\frac{3}{5}$。
现在,来逐一分析选项:
A. 顾客甲买了 $\frac{3}{5}$ kg,顾客乙买了 $\frac{3}{5}$ kg。
这与算式不符,因为算式中顾客乙买的数量是依赖于顾客甲买完后的剩余数量,而不是一个固定的数量。
B. 顾客甲买了 $\frac{3}{5}$(这里没有单位,理解为比例而非具体重量),顾客乙买了剩下的 $\frac{3}{5}$。
这个选项的表述有些模糊,且如果顾客甲买了 $\frac{3}{5}$ 的比例,那么算式应该是 $8 × (1-\frac{3}{5}) × (1-\frac{3}{5})$,与给定算式不符。
C. 这个选项与B类似,但顾客乙买的部分加了单位,这同样与算式不符。
D. 顾客甲买了 $\frac{3}{5}$ kg,顾客乙买了剩下的 $\frac{3}{5}$。
这与算式完全吻合。顾客甲先买了 $\frac{3}{5}$ kg,剩下 $8-\frac{3}{5}$ kg,然后顾客乙买了剩余数量的 $\frac{3}{5}$。
综上所述,答案是D。
本题考查的是分数的应用。
题目给出了一个算式 $(8-\frac{3}{5})×(1-\frac{3}{5})$,需要根据这个算式来补充横线上的条件。
首先,看到算式中有两个因子:$(8-\frac{3}{5})$ 和 $(1-\frac{3}{5})$。
第一个因子 $(8-\frac{3}{5})$ 表示原始数量 8 kg 减去一个确定的量 $\frac{3}{5}$ kg,这可以理解为顾客甲购买的数量。
第二个因子 $(1-\frac{3}{5})$ 表示剩余数量(即 $8-\frac{3}{5}$)再减去剩余数量的 $\frac{3}{5}$,这可以理解为顾客乙购买的数量是剩余数量的 $\frac{3}{5}$。
现在,来逐一分析选项:
A. 顾客甲买了 $\frac{3}{5}$ kg,顾客乙买了 $\frac{3}{5}$ kg。
这与算式不符,因为算式中顾客乙买的数量是依赖于顾客甲买完后的剩余数量,而不是一个固定的数量。
B. 顾客甲买了 $\frac{3}{5}$(这里没有单位,理解为比例而非具体重量),顾客乙买了剩下的 $\frac{3}{5}$。
这个选项的表述有些模糊,且如果顾客甲买了 $\frac{3}{5}$ 的比例,那么算式应该是 $8 × (1-\frac{3}{5}) × (1-\frac{3}{5})$,与给定算式不符。
C. 这个选项与B类似,但顾客乙买的部分加了单位,这同样与算式不符。
D. 顾客甲买了 $\frac{3}{5}$ kg,顾客乙买了剩下的 $\frac{3}{5}$。
这与算式完全吻合。顾客甲先买了 $\frac{3}{5}$ kg,剩下 $8-\frac{3}{5}$ kg,然后顾客乙买了剩余数量的 $\frac{3}{5}$。
综上所述,答案是D。
查看更多完整答案,请扫码查看


