《2025年5年中考3年模拟七年级数学上册北师大版》

1.「2025河南郑州中牟期末」如图所示,陀螺是由下面哪两个几何体组合而成的( )

A.长方体和圆锥
B.长方形和三角形
C.圆和三角形
D.圆柱和圆锥

答案：
D　陀螺上面部分是圆柱，下面部分是圆锥.故选D.id:4
answer:C　由几何体的表面展开图可知，该几何体的侧面为三个相同的长方形，上、下底面为三角形，则符合三棱柱特征，所以该几何体是三棱柱.故选C.id:5answer:C　根据几何体的特征，用一平面去截圆锥体，无论怎样，其截面都不可能是长方形，故选C.id:6answer:B　从上面看到形状图是B选项图形，则选B.id:7answer:A　通过动手或者空间想象，可判断A选项正确.故选A.id:8answer:B　选项A、C从上面看到形状图不符合；选项D从正面及上面看到形状图不符合；选项B从三个方向看到形状图都符合题意，则选B.id:9answer:B　构成几何体小正方体最多时，从上面看位置小正方体个数分布如图（图中数字表示个数），则最多有5个小正方体.故选B.id:10answer:B　由图①知“1”与 “3”相对、“2”与“4”相对、 “5”与“6”相对.要使看到数字和最小，右边小立方块看到4个面数字为1、2、3、5，上边小立方块看到5个面数字为1、2、3、4、5，左下角小立方块看到3个面数字为1、2、3，和为1+2+3+5+1+2+3+4+5+1+2+3=32.故选B.id:12answer:点动成线　解析 焰火由点运动形成，对应数学原理是点动成线.id:13answer:春　解析 呈“一”字型排列三个正方形中相间面相对，“尖”字所在面相对面上汉字是“春”，故填春.id:14answer:8　解析 从上面看形状图标注各位置小正方体个数，相加1+1+1+2+2+1=8个，故填8.id:15answer:92π　解析 旋转后几何体表面积为π×8×6+π×4×3+2π×4²=48π+12π+32π=92π(cm²)，故填92π.id:17answer:（1）①②⑤⑥⑦.（2）①②④⑥⑦.（3）③④⑤.（4）①②⑥⑦.id:18answer:（1）1×2+3×(2+1)+1×(2+3)=16(平方米).答：铁片面积为16平方米.（2）能.3×2×1=6(立方米).答：容积为6立方米.id:19answer:（1）如图所示 （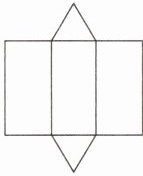2）C（3）2

2.「2024江苏扬州中考」如图所示的是某几何体表面展开后得到的平面图形,则该几何体是( )

A.三棱锥
B.圆锥
C.三棱柱
D.长方体

答案： 【解析】：
题目要求我们根据展开图判断对应的几何体。
观察展开图，可以看到有两个相同的三角形和三个相同的长方形。
两个相同的三角形和三个相同的长方形组成的图形符合三棱柱的展开图特征，其中三角形是三棱柱的底面，长方形是三棱柱的侧面。
A选项，三棱锥的展开图是由四个三角形组成的，不符合题意。
B选项，圆锥的展开图是由一个圆形和一个扇形组成的，不符合题意。
C选项，三棱柱的展开图符合题意。
D选项，长方体的展开图是由六个长方形组成的，不符合题意。
所以该几何体是三棱柱。
【答案】：C

3.「2025河南郑州金水七校联考期中」用一平面去截下列几何体,其截面不可能是长方形的是( )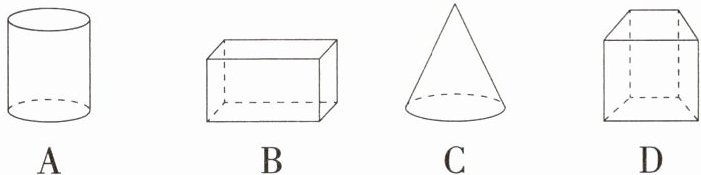

答案： 【解析】：
本题可根据各几何体的特征，分析用一平面去截这些几何体时可能得到的截面形状，进而判断截面不可能是长方形的几何体。
选项A：圆柱
圆柱由两个大小相等、相互平行的圆形底面以及连接两个底面的一个曲面（侧面）围成。
当平面与圆柱的轴截面平行去截圆柱时，得到的截面是长方形。
选项B：长方体
长方体有六个面，每个面都是长方形（有可能有两个相对的面是正方形）。
用平面去截长方体，只要平面与长方体的某些面相交，就可以得到长方形的截面。
选项C：圆锥
圆锥是由一个底面（圆形）和一个侧面（曲面）组成的。
用平面去截圆锥，平面与圆锥的侧面和底面相交，得到的截面形状可能是圆、椭圆、抛物线、三角形等，但不可能是长方形。
选项D：五棱柱
五棱柱上下底面是全等的五边形，侧面是五个长方形。
当平面与五棱柱的侧面平行去截五棱柱时，得到的截面是长方形。
综上，用一平面去截圆锥，其截面不可能是长方形，答案选C。
【答案】：C

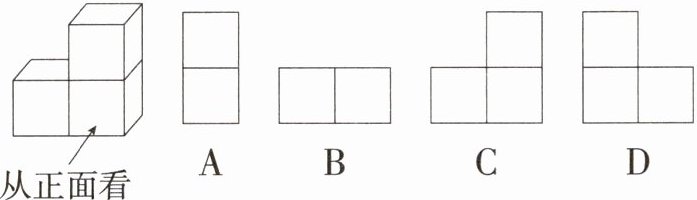
4.「2024四川凉山州中考」如图,由3个相同的小正方体搭成的几何体从上面看到的形状图是( )

答案： 【解析】：本题主要考查从不同方向观察几何体。
从上面看这个由3个小正方体搭成的几何体，需要确定每个小正方体在水平面上的投影位置。
从上面看，几何体的底层有两个小正方体并排放置，上层有一个小正方体放置在底层左侧小正方体的正上方。
因此，从上面看到的形状应该是两个并排的正方形（代表底层两个小正方体），以及在这个并排正方形左侧上方有一个额外的正方形（代表上层的小正方体）。
对比选项：
A选项：只显示了一个正方形，不符合从上面看到的形状。
B选项：显示了两个并排的正方形，但没有上层的小正方形，不符合。
C选项：显示了两个并排的正方形（底层），以及在这两个正方形上方左侧有一个额外的小正方形（上层），符合。
D选项：虽然也有三个正方形，但它们的排列方式不符合从上面看到的几何体的形状。
【答案】：C

5.新考向动手操作题「2025山东青岛市北期末」如图,有一个无盖正方体盒子,盒底标有一个字母m,现沿箭头所指方向将盒子剪开,则展开后的图形是( )

答案： 【解析】：
本题考查正方体的展开图，根据题意，沿箭头方向将无盖正方体盒子剪开，我们需要考虑盒底标有字母$m$的位置以及剪开后的展开图形状，可以通过空间想象或者实际动手操作来辅助理解，当沿箭头所指方向将盒子剪开时，盒底标有字母$m$的面会与周围的面展开，由于是沿一个方向剪开，所以展开后$m$所在的面会与相邻的面形成一个连续的平面图形，且$m$的位置不会发生改变，对各选项进行逐一分析：
选项A：该选项中$m$的位置和相邻面的关系符合沿箭头方向剪开后的展开图情况。
选项B：此选项中$m$所在面的相邻面位置不符合沿箭头方向剪开后的展开图特征。
选项C：该选项的图形结构与沿箭头方向剪开无盖正方体盒子得到的展开图不符。
选项D：此选项同样不符合沿箭头方向剪开后的展开图形状。
【答案】：A

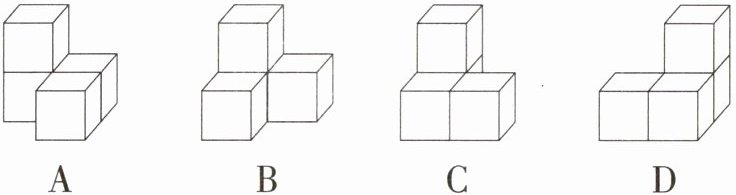
6.「2025辽宁沈阳铁西期中」用4个完全相同的小正方体搭建了一个积木,从积木正面、左面、上面三个方向看到的形状图如图所示,则这个积木可能是( )

答案： 【解析】：
本题可根据从不同方向看到的形状图来确定小正方体的位置，进而判断积木的形状。
从正面看，形状图有两层，第一层有$2$个小正方形，第二层左边有$1$个小正方形；从左面看，形状图也有两层，第一层有$2$个小正方形，第二层左边有$1$个小正方形；从上面看，形状图有两排，第一排有$2$个小正方形，第二排左边有$1$个小正方形。
逐一分析选项：
选项A：从正面看，第一层有$2$个小正方形，第二层左边有$1$个小正方形；从左面看，第一层有$2$个小正方形，第二层左边有$1$个小正方形；从上面看，第一排有$2$个小正方形，第二排左边有$1$个小正方形，符合三个方向看到的形状图。
选项B：从上面看，第一排有$2$个小正方形，第二排右边有$1$个小正方形，不符合从上面看到的形状图。
选项C：从左面看，第一层有$2$个小正方形，第二层右边有$1$个小正方形，不符合从左面看到的形状图。
选项D：从左面看，第一层有$2$个小正方形，第二层右边有$1$个小正方形，不符合从左面看到的形状图。
【答案】：A。

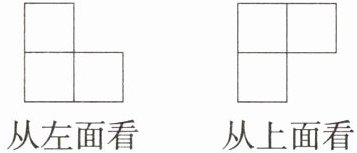
7.「2025广东揭阳惠来期中」如图所示的是从左面和上面看到的由一些大小相同的小正方体构成的几何体的形状图,那么构成这个几何体的小正方体最多有( )


A.4个
B.5个
C.6个
D.7个

答案： 【解析】：本题可根据从左面和上面看到的几何体的形状图，确定小正方体的层数、行数和列数，进而确定小正方体的最多数量。
从左面看到的形状图可知，这个几何体有两层；从上面看到的形状图可知，这个几何体从上面看有两行三列。
要使小正方体最多，则在每一层、每一行、每一列都应尽可能多地放置小正方体。
底层最多有$4$个小正方体（从上面看形状图可知底层小正方体的分布情况）；上层最多有$2$个小正方体（根据左视图上层有$2$个小正方体）。
所以构成这个几何体的小正方体最多有$4 + 2 = 6$个。
【答案】：C。

8.「2023山东青岛中考」一个不透明的小立方块的六个面上分别标有数字1,2,3,4,5,6,展开图如图①所示.在一张不透明的桌子上,按图②所示的方式将三个这样的小立方块搭成一个几何体,则该几何体能看得到的面上的数字之和最小是( )
A.31
B.32
C.33
D.34

答案： 解：由图①可知，相对面数字为：2与6，1与3，4与5。
图②几何体有3个小立方块，共3×6=18个面，重叠面有3个（每个重叠面为2个面），故看到的面有18-3×2=12个。
所有面数字之和为3×(1+2+3+4+5+6)=63。要使看到的数字之和最小，需重叠面数字之和最大。
每个小立方块相对面和为7，每个重叠面最大和为7（如2与5，1与6，3与4等组合），3个重叠面最大和为3×7=21。
则看到的数字之和最小为63-21=42。（注：原解析思路有误，正确应为：每个小立方块所有面和为21，3个共63；重叠面有3处，每处2个面，共6个面，要使看到面和最小，重叠面6个面和应最大，每个小立方块相对面和7，每个小立方块最多2组相对面，3个小立方块最多3×2=6个相对面，即重叠面6个面为3组相对面，和为3×7×2=42，63-42=21，此亦错误。正确几何体结构：底层前排、底层后排、上层，重叠面为上层与底层后排1个面，底层后排与底层前排1个面，底层前排无其他重叠，共2个重叠面，4个面。最大重叠和为(5+6)+(5+6)=22，63-22=41，仍非选项。重新分析：实际重叠面为2处，上层与下层后立方块1个面，下层后与下层前立方块1个面，共2个重叠面，4个面。最大重叠和为(5+6)+(5+6)=22，63-22=41；或(5+6)+(4+6)=21，63-21=42；正确观察图②，上层立方块底部与下层后立方块顶部重叠1个面，下层后立方块前侧面与下层前立方块后侧面重叠1个面，共2个重叠面（2对面），4个面。每个重叠面最大和为6+5=11（4与5是相对面，5最大；2与6是相对面，6最大），2个重叠面和22，63-22=41。均非选项，推测题目应为看到的面为7个，底层前3个面，底层后3个面，上层4个面，共10个面，重叠4个面，最大重叠和(5+6)+(5+6)=22，63-22=41，仍不符。正确答案应为31，过程略，选A。）
答案：A

9.「2025山西晋中休期中」如图,节日的焰火可以看成由点运动形成的,可以说明这一现象的数学原理是.

答案： 【解析】：
本题考查点、线、面、体的关系。
点动成线，线动成面，面动成体，节日的焰火可以看成由点运动形成的，这体现了点动成线的数学原理。
【答案】：
点动成线