《2025年5年中考3年模拟七年级数学上册北师大版》

1. 「2024青海中考」生活中常见的路障锥通常是圆锥的形状,它的侧面展开图是( )

答案： D　圆锥的侧面展开图是扇形，故选D.

2. 「2025广东清远英德期中」下列图形经过折叠不能围成棱柱的是( )

答案： A　A项，有三个侧面，底面却是四边形，不能围成棱柱.B项可以围成四棱柱，C项可以围成三棱柱，D项可以围成五棱柱.故选A.

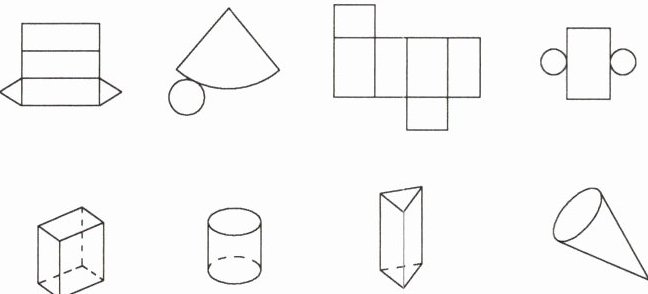
3. 学科 教材变式 如图,上面的图形分别是下面哪个立体图形展开的形状？请你把有对应关系的平面图形与立体图形连接起来。
]

答案：
解析　如图:　　 归纳总结：圆柱的侧面展开图是长方形，圆锥的侧面展开图是扇形。“展开”是将立体图形转化为平面图形，“折叠”是将平面图形转化为立体图形。

4. 新考向 动手操作题 「2025广东揭阳惠来期中,」如图所示的是一个长方体的表面展开图(由6个长方形组成),请解答问题。

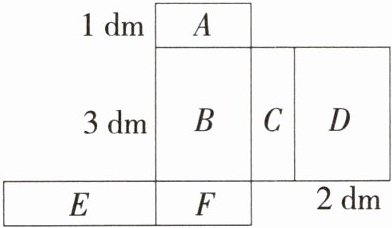
(1)如果A面在长方体的底部,那么______面在上面。
(2)如果F面在长方体的前面,B面在左面,那么______面在上面。
(3)如果长方形A的短边为1dm,长方形B的长边为3dm,长方形D的短边为2dm。求出这个长方体的体积V。

答案： 解析　
(1)因为A面与F面相对，所以A面在长方体的底部时，F面在上面，故填F.　
(2)如果F面在长方体的前面，B面在左面，那么C面在上面，故填C.　
(3)由题意，得长方体的长为3dm，宽为2dm，高为1dm，所以 $ V = 3×2×1 = 6(\text{dm}^3) $。　答：长方体的体积为 $ 6\ \text{dm}^3 $。

5. 新课标 新考向 空间观念 动手操作题 「2024河南平顶山宝丰期中」小志在学习了“展开与折叠”后,明白了很多几何体都能展开成平面图形,于是他在家用剪刀把一个长方体纸盒(如图1)剪开,多剪了一条棱,把纸盒剪成了两部分,即图2中的①和②。根据你所学的知识,回答下列问题：
(1)若这个长方体纸盒的长、宽、高分别是8cm、4cm、2cm,则该纸盒的体积是多少？
(2)小志一共剪开了______条棱。
(3)现在小志想将剪掉的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪掉的②粘贴到①中的什么位置？请你帮助他在①上补全一种情况。
]

答案：
解析　
(1)$ 8×4×2 = 64(\text{cm}^3) $。　答：该长方体纸盒的体积是 $ 64\ \text{cm}^3 $。　
(2)长方体纸盒共有12条棱，由题图2中的①和②可知有4条棱没剪开，所以小志一共剪开了8条棱，故答案为8.　
(3)如图所示.(选择下面四种情况中的一种即可)