第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1.「2025福建泉州期末」下列说法错误的是 ( )
A.直线AB和直线BA表示同一条直线
B.过一点能作无数条直线
C.射线AB和射线BA表示不同射线
D.射线比直线短
A.直线AB和直线BA表示同一条直线
B.过一点能作无数条直线
C.射线AB和射线BA表示不同射线
D.射线比直线短
答案:
D A、B、C选项的说法都正确;射线、直线都是无限长的,不能比较长短,故D选项的说法错误.故选D.
2.同一平面内有A,B,C三点,经过任意两点画直线,共可画 ( )
A.1条
B.3条
C.1条或3条
D.不能确定
A.1条
B.3条
C.1条或3条
D.不能确定
答案:
C 如图,同一平面内有A,B,C三点,经过任意两点画直线,共可画1条或3条.故选C.

C 如图,同一平面内有A,B,C三点,经过任意两点画直线,共可画1条或3条.故选C.

3.「2024山东菏泽成武期中」图中共有______条不同的线段.


答案:
答案 10
解析 题图中的线段有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE,共10条.
解析 题图中的线段有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE,共10条.
4.「2025北京朝阳期末」如图,下列表述点与直线关系的语句:①点A在直线BC外;
②直线m和n相交于点C;
③点B既在直线l上又在直线m上.其中正确的是______(直接填写序号).
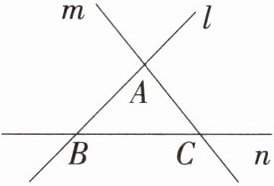
②直线m和n相交于点C;
③点B既在直线l上又在直线m上.其中正确的是______(直接填写序号).

答案:
答案 ①②
解析 ①②中的表达都正确;③点B既在直线l上又在直线n上,故③错误.
解析 ①②中的表达都正确;③点B既在直线l上又在直线n上,故③错误.
5.王小毛同学做教室卫生时,发现座位很不整齐,他思考了一下,将第一个座位和最后一个座位固定之后,沿着这条线就把座位摆整齐了!他利用了数学原理:______.
答案:
答案 两点确定一条直线
6.学科教材变式 学科易错题「2025安徽淮南期末,★☆」如图,已知A,B,C,D四个点.
(1)画直线AB,CD相交于点P.
(2)连接AC和BD并延长AC和BD相交于点Q.
(3)连接AD,BC相交于点O.
(4)以点C为端点的射线有______条.
(5)以点C为一个端点的线段有______条.
(1)画直线AB,CD相交于点P.
(2)连接AC和BD并延长AC和BD相交于点Q.
(3)连接AD,BC相交于点O.
(4)以点C为端点的射线有______条.
(5)以点C为一个端点的线段有______条.
答案:
解析
(1)
(2)
(3)如图所示.

(4)3.详解:以点C为端点的射线有3条,分别是射线CP,CD,CQ.
(5)6.详解:以点C为一个端点的线段有6条,分别是线段CP,CD,CA,CQ,CO,CB.
易错警示 画“三线”的注意点:①画线段时,要确定哪两个点是端点,不能画“出头”,还要注意延长线与反向延长线的区别;②画射线时,要注意射线的端点和延伸的方向;③画直线时,要注意直线没有端点,可以向两个方向无限延伸,要画“出头”.
解析
(1)
(2)
(3)如图所示.

(4)3.详解:以点C为端点的射线有3条,分别是射线CP,CD,CQ.
(5)6.详解:以点C为一个端点的线段有6条,分别是线段CP,CD,CA,CQ,CO,CB.
易错警示 画“三线”的注意点:①画线段时,要确定哪两个点是端点,不能画“出头”,还要注意延长线与反向延长线的区别;②画射线时,要注意射线的端点和延伸的方向;③画直线时,要注意直线没有端点,可以向两个方向无限延伸,要画“出头”.
7.阅读下列材料并填空:
(1)探究:平面内有n个点$(n≥2)$且任意3个点不在同一条直线上,经过每两点画一条直线,一共能画多少条直线?
我们知道,两点确定一条直线.平面内有2个点时,可以画$\frac {2×1}{2}= 1$条直线,平面内有3个点时,一共可以画$\frac {3×2}{2}= 3$条直线,平面内有4个点时,一共可以画$\frac {4×3}{2}= 6$条直线,平面内有5个点时,一共可以画______条直线,……,平面内有n个点时,一共可以画______条直线.
(2)运用:某足球比赛中有22个球队进行单循环比赛(每两队之间必须比赛一场),一共要进行多少场比赛?
(1)探究:平面内有n个点$(n≥2)$且任意3个点不在同一条直线上,经过每两点画一条直线,一共能画多少条直线?
我们知道,两点确定一条直线.平面内有2个点时,可以画$\frac {2×1}{2}= 1$条直线,平面内有3个点时,一共可以画$\frac {3×2}{2}= 3$条直线,平面内有4个点时,一共可以画$\frac {4×3}{2}= 6$条直线,平面内有5个点时,一共可以画______条直线,……,平面内有n个点时,一共可以画______条直线.
(2)运用:某足球比赛中有22个球队进行单循环比赛(每两队之间必须比赛一场),一共要进行多少场比赛?
答案:
解析
(1)$\frac{5×4}{2}=10$;$\frac{n(n-1)}{2}$.
(2)$\frac{22×21}{2}=231$.
答:一共要进行231场比赛.
方法技巧 两点确定一条直线,两点确定一条线段,两条直线有一个交点,……,在数学本质上,它们可以转化为一类问题,即每两个要素确定一个基本图形(或一个组合)的问题.解决这类问题的通用方法:若有n个要素,则组成的基本图形(或组合)的数目为$\frac{n(n-1)}{2}$.
(1)$\frac{5×4}{2}=10$;$\frac{n(n-1)}{2}$.
(2)$\frac{22×21}{2}=231$.
答:一共要进行231场比赛.
方法技巧 两点确定一条直线,两点确定一条线段,两条直线有一个交点,……,在数学本质上,它们可以转化为一类问题,即每两个要素确定一个基本图形(或一个组合)的问题.解决这类问题的通用方法:若有n个要素,则组成的基本图形(或组合)的数目为$\frac{n(n-1)}{2}$.
查看更多完整答案,请扫码查看


