第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
9. [ ]如图,$△ABC和△DEF的面积分别为S_{1},$ $S_{2}$,则 ( )

A.$S_{1}>S_{2}$
B.$S_{1}<S_{2}$
C.$S_{1}= S_{2}$
D.无法确定

A.$S_{1}>S_{2}$
B.$S_{1}<S_{2}$
C.$S_{1}= S_{2}$
D.无法确定
答案:
C 如图1,过点A作AG⊥BC于G;在Rt△ABG中,AG =AB·sin40°=5sin40°,
∴S₁=$\frac{1}{2}$BC·AG=$\frac{1}{2}$×8×5sin40°=20sin40°。
如图2,过点D作DH⊥EF,交FE的延长线于H。在Rt△DHE中,∠DEH=180° - ∠DEF=40°,
∴DH=DE·sin∠DEH=8sin40°,
∴S₂=$\frac{1}{2}$EF·DH=$\frac{1}{2}$×5×8sin40°=20sin40°,
∴S₁=S₂。故选C。


C 如图1,过点A作AG⊥BC于G;在Rt△ABG中,AG =AB·sin40°=5sin40°,
∴S₁=$\frac{1}{2}$BC·AG=$\frac{1}{2}$×8×5sin40°=20sin40°。
如图2,过点D作DH⊥EF,交FE的延长线于H。在Rt△DHE中,∠DEH=180° - ∠DEF=40°,
∴DH=DE·sin∠DEH=8sin40°,
∴S₂=$\frac{1}{2}$EF·DH=$\frac{1}{2}$×5×8sin40°=20sin40°,
∴S₁=S₂。故选C。


10. [2023 湖北武汉中考, ]如图,将$45^{\circ }的∠AOB$ 按下面的方式放置在一把刻度尺上,顶点 O 与尺下沿的端点重合,OA 与尺下沿重合,OB 与尺上沿的交点 B 在尺上的读数为 2 cm,若按相同的方式将$37^{\circ }的∠AOC$放置在该刻度尺上,则 OC 与尺上沿的交点 C 在尺上的读数约是 _ cm(结果精确到 0.1 cm,参考数据: $sin37^{\circ }\approx 0.60,cos37^{\circ }\approx 0.80,tan37^{\circ }\approx 0.75).$


答案:
答案 2.7
解析 如图,过点B作BD⊥OA于D,过点C作CE⊥OA于E,在△BOD中,∠BDO=90°,∠DOB=45°,
∴BD=OD=2cm,
∴CE=2cm。在△OCE中∠COE =37°,∠CEO=90°,
∴tan37°=$\frac{CE}{OE}$≈0.75,
∴OE≈2.7cm,即OC与尺上沿的交点C在尺上的读数约是2.7cm。

答案 2.7
解析 如图,过点B作BD⊥OA于D,过点C作CE⊥OA于E,在△BOD中,∠BDO=90°,∠DOB=45°,
∴BD=OD=2cm,
∴CE=2cm。在△OCE中∠COE =37°,∠CEO=90°,
∴tan37°=$\frac{CE}{OE}$≈0.75,
∴OE≈2.7cm,即OC与尺上沿的交点C在尺上的读数约是2.7cm。

11. [2023 安徽怀远期末, ]如图,在$Rt△ABC$中, $∠ACB= 90^{\circ }$,AD 平分$∠BAC$交 BC 边于点 D, $DE⊥AB$于点 E,若$BD= 5,cosB= \frac {4}{5}$,求 AC 的长.


答案:
解析 在Rt△BDE中,cosB=$\frac{BE}{BD}$=$\frac{4}{5}$,
∵BD=5,
∴BE=4,
∴DE=$\sqrt{BD² - BE²}$=$\sqrt{5² - 4²}$=3。
∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴CD=3,
∴BC=5 + 3=8。
∵在Rt△ABC中,∠C=90°,cosB=$\frac{BC}{AB}$=$\frac{4}{5}$,
∴$\frac{8}{AB}$=$\frac{4}{5}$,
∴AB=10,
∴AC=$\sqrt{10² - 8²}$=6。
∵BD=5,
∴BE=4,
∴DE=$\sqrt{BD² - BE²}$=$\sqrt{5² - 4²}$=3。
∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴CD=3,
∴BC=5 + 3=8。
∵在Rt△ABC中,∠C=90°,cosB=$\frac{BC}{AB}$=$\frac{4}{5}$,
∴$\frac{8}{AB}$=$\frac{4}{5}$,
∴AB=10,
∴AC=$\sqrt{10² - 8²}$=6。
12. [2024 山东潍坊期中, ]如图,在$△ABC$中,$∠B$ $=60^{\circ },∠BAC= 75^{\circ },AB= 2$.点 D 在 BC 的延长线上,且$CD= CA$,连接 AD.
(1)求 BC 的长.
(2)求$tanD$的值.
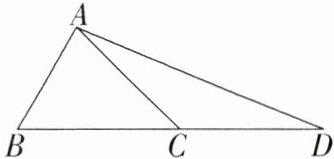
(1)求 BC 的长.
(2)求$tanD$的值.

答案:
解析
(1)如图,过点A作AE⊥BC于点E,在Rt△ABE中,∠B=60°,∠AEB=90°,AB=2,
∴BE=AB·cosB=1,AE=AB·sinB=$\sqrt{3}$。
∵在△ABC中,∠B=60°,∠BAC=75°,
∴∠ACB=180° - ∠B - ∠BAC=45°。在Rt△ACE中,CE=$\frac{AE}{tan∠ACE}$=$\sqrt{3}$,
∴BC=BE + CE=1 + $\sqrt{3}$。

(2)在Rt△AEC中AC=$\frac{AE}{sin∠ACE}$=$\sqrt{6}$,
∴AC=CD=$\sqrt{6}$,
∴DE=CE + CD=$\sqrt{3}$ + $\sqrt{6}$。在Rt△AED中,tanD=$\frac{AE}{DE}$=$\frac{\sqrt{3}}{\sqrt{3} + \sqrt{6}}$=$\sqrt{2}$ - 1。
解析
(1)如图,过点A作AE⊥BC于点E,在Rt△ABE中,∠B=60°,∠AEB=90°,AB=2,
∴BE=AB·cosB=1,AE=AB·sinB=$\sqrt{3}$。
∵在△ABC中,∠B=60°,∠BAC=75°,
∴∠ACB=180° - ∠B - ∠BAC=45°。在Rt△ACE中,CE=$\frac{AE}{tan∠ACE}$=$\sqrt{3}$,
∴BC=BE + CE=1 + $\sqrt{3}$。

(2)在Rt△AEC中AC=$\frac{AE}{sin∠ACE}$=$\sqrt{6}$,
∴AC=CD=$\sqrt{6}$,
∴DE=CE + CD=$\sqrt{3}$ + $\sqrt{6}$。在Rt△AED中,tanD=$\frac{AE}{DE}$=$\frac{\sqrt{3}}{\sqrt{3} + \sqrt{6}}$=$\sqrt{2}$ - 1。
13. [2024 安徽蚌埠二模, ]如图,在四边形 ABCD 中,$∠DAB= 90^{\circ },∠ADC= 120^{\circ },∠ABC= 70^{\circ },$ $BC= 80,CD= 100$,求 AB 的长.(结果取整数, 参考数据:$sin20^{\circ }\approx 0.34,cos20^{\circ }\approx 0.94,\sqrt {3}\approx $ 1.732)


答案:
解:过点C作CE⊥AB于点E,过点D作DF⊥CE于点F。
在Rt△CDF中,∠CDF=180°-∠ADC=60°,CD=100,
CF=CD·sin60°=100×(√3/2)=50√3≈86.6,
DF=CD·cos60°=100×0.5=50。
在Rt△BCE中,∠BCE=90°-∠ABC=20°,BC=80,
CE=BC·cos20°≈80×0.94=75.2,
BE=BC·sin20°≈80×0.34=27.2。
EF=CF-CE≈86.6-75.2=11.4。
∵∠DAB=∠AFD=∠AEF=90°,
∴四边形ADFE为矩形,
∴AB=AE+BE=DF+BE≈50+27.2=77.2≈77。
答:AB的长约为77。
在Rt△CDF中,∠CDF=180°-∠ADC=60°,CD=100,
CF=CD·sin60°=100×(√3/2)=50√3≈86.6,
DF=CD·cos60°=100×0.5=50。
在Rt△BCE中,∠BCE=90°-∠ABC=20°,BC=80,
CE=BC·cos20°≈80×0.94=75.2,
BE=BC·sin20°≈80×0.34=27.2。
EF=CF-CE≈86.6-75.2=11.4。
∵∠DAB=∠AFD=∠AEF=90°,
∴四边形ADFE为矩形,
∴AB=AE+BE=DF+BE≈50+27.2=77.2≈77。
答:AB的长约为77。
查看更多完整答案,请扫码查看


