《2025年5年中考3年模拟九年级数学上册沪科版》

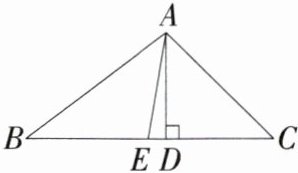
10.「2024浙江中考,」如图,在$\triangle ABC$中,$AD\perp BC$,$AE是BC$边上的中线,$AB = 10$,$AD = 6$,$\tan∠ACB = 1$.
(1)求$BC$的长.
(2)求$\sin∠DAE$的值.

答案：
(1)
∵AD⊥BC，AB=10，AD=6，
∴在Rt△ABD中，BD=$\sqrt{AB^{2}-AD^{2}}$=$\sqrt{10^{2}-6^{2}}$=8。
∵tan∠ACB=1，
∴$\frac{AD}{CD}$=1，
∴CD=AD=6，
∴BC=BD+CD=8+6=14。
(2)
∵AE是BC边上的中线，
∴CE=$\frac{1}{2}$BC=7，
∴DE=CE−CD=7−6=1，
∴在Rt△AED中，AE=$\sqrt{AD^{2}+DE^{2}}$=$\sqrt{6^{2}+1^{2}}$=$\sqrt{37}$，
∴sin∠DAE=$\frac{DE}{AE}$=$\frac{1}{\sqrt{37}}$=$\frac{\sqrt{37}}{37}$。

11. 运算能力 新定义题 我们定义：等腰三角形中底边与腰的比叫做底角的邻对($\text{can}$),如图1,在$\triangle ABC$中,$AB = AC$,底角$B的邻对记作\text{can}B$,这时$\text{can}B= \frac{\text{底边}}{\text{腰}}= \frac{BC}{AB}$.根据上述底角的邻对的定义,解答下列问题：
(1)$\text{can}30^{\circ}=$____.(提示：$\cos30^{\circ}=\frac{\sqrt{3}}{2}$)
(2)如图2,已知在$\triangle ABC$中,$AB = AC$,$\text{can}B= \frac{8}{5}$,$S_{\triangle ABC}= 24$,求$\triangle ABC$的周长.

答案：
(1)$\sqrt{3}$
(2)过点A作AE⊥BC于点E，如图2，
∵tanB=$\frac{8}{5}$，
∴可设BC=8x，AB=5x，x＞0，易知BE=$\frac{1}{2}$BC=4x，
∴AE=$\sqrt{AB^{2}-BE^{2}}$=3x，
∵S△ABC=24，
∴$\frac{1}{2}$BC·AE=$\frac{1}{2}$·8x·3x=24，解得x1=$\sqrt{2}$，x2=−$\sqrt{2}$(舍去)，
∴AB=AC=5$\sqrt{2}$，BC=8$\sqrt{2}$，
∴△ABC的周长=AB+AC+BC=5$\sqrt{2}$+5$\sqrt{2}$+8$\sqrt{2}$=18$\sqrt{2}$。

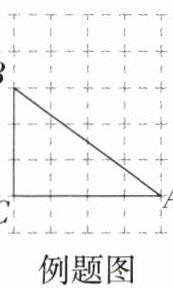
例题 「2024山东济南期末」如图,在由边长为$1$的小正方形组成的网格中,点$A$,$B$,$C$都在格点上,则$\tan B$的值为( )

A.$\frac{3}{4}$
B.$\frac{4}{3}$
C.$\frac{3}{5}$


D.$\frac{4}{5}$

答案： 由题图得，AC=4，BC=3，∠C=90°，
∴tanB=$\frac{AC}{BC}$=$\frac{4}{3}$，故选B。

变式1【两边在格线上变成一边在格线上】
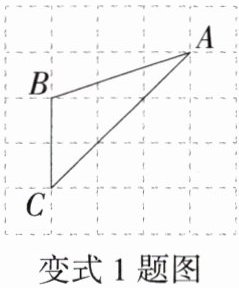
多解法 如图,$\triangle ABC的三个顶点均在由边长为1$的小正方形组成的网格的格点上,则$\cos A$的值为( )

A.$\frac{1}{2}$
B.$\frac{\sqrt{5}}{5}$
C.$2$
D.$\frac{2\sqrt{5}}{5}$

答案： D 【解法一】如图，取格点D，由图易知点D在AC上，连接BD，由勾股定理得，AB=$\sqrt{1^{2}+3^{2}}$=$\sqrt{10}$，AD =$\sqrt{2^{2}+2^{2}}$=2$\sqrt{2}$，BD=$\sqrt{1^{2}+1^{2}}$=$\sqrt{2}$，
∵AD²+BD²=10，AB²=10，
∴AD²+BD²=AB²，
∴△ABD是直角三角形，且∠ADB=90°，
∴cosA=$\frac{AD}{AB}$=$\frac{2\sqrt{2}}{\sqrt{10}}$=$\frac{2\sqrt{5}}{5}$，故选D。【解法二】如图，过点B作BD⊥AC，由勾股定理得，AB=$\sqrt{1^{2}+3^{2}}$=$\sqrt{10}$，AC=$\sqrt{3^{2}+3^{2}}$=3$\sqrt{2}$，
∴S△ABC=$\frac{1}{2}$BC×3=$\frac{1}{2}$AC·BD，即$\frac{1}{2}$×2×3=$\frac{1}{2}$×3$\sqrt{2}$BD，
∴BD=$\sqrt{2}$，
∴AD=$\sqrt{AB^{2}-BD^{2}}$=$\sqrt{(\sqrt{10})^{2}-(\sqrt{2})^{2}}$=2$\sqrt{2}$，
∴cosA=$\frac{AD}{AB}$=$\frac{2\sqrt{2}}{\sqrt{10}}$=$\frac{2\sqrt{5}}{5}$，故选D。

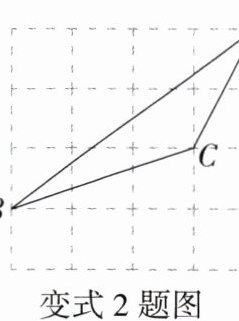
变式2 如图,在$4×4$的正方形网格中,每个小正方形的边长均为$1$,若$\triangle ABC$的顶点均在格点上,则$\sin∠CBA$的值是____.

答案： $\frac{\sqrt{10}}{10}$

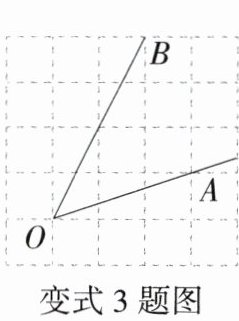
变式3【需要构造三角形】「2024广东揭阳揭东一模」如图,$∠AOB$是放置在正方形网格中的一个角,则$\cos∠AOB$的值是____.

答案： $\frac{\sqrt{2}}{2}$