《2025年5年中考3年模拟九年级数学上册沪科版》

1.「2024安徽亳州利辛开学测试」如图,在$\triangle ABC和\triangle ADE$中,$∠BAD= ∠CAE$,要使$\triangle ABC与\triangle ADE$相似,还需要满足下列条件中的( )

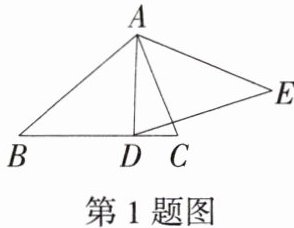
A.$\frac {AB}{AE}= \frac {AC}{AD}$
B.$\frac {AB}{AE}= \frac {BC}{DE}$
C.$\frac {AC}{AD}= \frac {BC}{DE}$
D.$\frac {AC}{AD}= \frac {AB}{DE}$

答案： A
∵∠BAD=∠CAE,
∴∠BAC=∠DAE,
∵$\frac{AB}{AE}=\frac{AC}{AD}$,
∴△ABC∽△AED.故选A.

2.「2025安徽宣城六校月考」如图,D,E分别是$\triangle ABC$的边AC,AB上的点,$AE= 1.5,AC= 2,BC= 4$,且$\frac {AD}{AB}= \frac {3}{4}$,则DE的长是( )

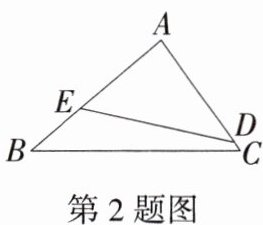
A.4
B.3
C.2
D.1

答案： B
∵D,E分别是△ABC的边AC,AB上的点,AE=1.5,AC=2,
∴$\frac{AE}{AC}=\frac{1.5}{2}=\frac{3}{4}$.
∵$\frac{AD}{AB}=\frac{3}{4}$,
∴$\frac{AE}{AC}=\frac{AD}{AB}$.又
∵∠DAE=∠BAC,
∴△DAE∽△BAC,
∴$\frac{DE}{BC}=\frac{3}{4}$.
∵BC=4,
∴DE=3.故选B.

3.「2025安徽六安月考」如图,在四边形ABCD中,AC平分$∠BAD$,且$AB= 4,AC= 6$.当$AD= $____时,$\triangle ABC\backsim \triangle ACD$.

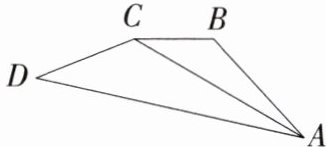
答案： 答案　9
　解析
∵AC平分∠BAD,
∴∠BAC=∠DAC,当$\frac{AB}{AC}=\frac{AC}{AD}$,即$AC^2=AB\cdot AD$时,△ABC∽△ACD.
∵AB=4,AC =6,
∴$6^2=4AD$,
∴AD=9.

4.「2023江苏镇江中考」如图,用一个卡钳$(AD= BC,\frac {OC}{OB}= \frac {OD}{OA}= \frac {1}{3})$测量某个零件的内孔直径AB,量得CD的长度为6cm,则AB的长度为____cm.

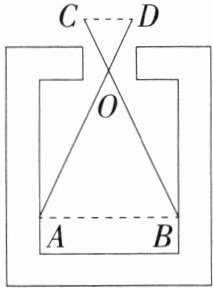
答案： 答案　18
　解析
∵$\frac{OC}{OB}=\frac{OD}{OA}=\frac{1}{3}$,∠COD=∠AOB,
∴△COD∽△BOA,
∴AB:CD=3.
∵CD=6cm,
∴AB=6×3=18(cm).

5.学科 母子型 学科 教材变式 「2024安徽安庆宿松期中」如图,在$\triangle ABC$中,点D是AB上的一点,且$AD= 2,AB= 6,AC= 2\sqrt {3},CD= 5$.求BC的长.

答案： 解析
∵AD=2,AB=6,AC=$2\sqrt{3}$,
∴$\frac{AD}{AC}=\frac{2}{2\sqrt{3}}=\frac{\sqrt{3}}{3}$,$\frac{AC}{AB}=\frac{2\sqrt{3}}{6}=\frac{\sqrt{3}}{3}$,
∴$\frac{AC}{AB}=\frac{AD}{AC}$.又
∵∠A=∠A,
∴△ACD∽△ABC,
∴$\frac{CD}{BC}=\frac{AD}{AC}$,即$\frac{5}{BC}=\frac{2}{2\sqrt{3}}$,
∴BC=$5\sqrt{3}$.

6.如图,在$\triangle ABC$中,点D,E分别在边AB,AC上,$∠AED= ∠B$,线段AG分别交线段DE,BC于点F,G,且$\frac {AD}{AC}= \frac {DF}{CG}$.
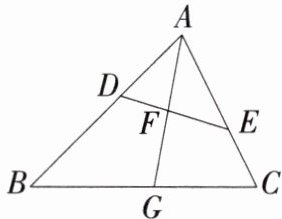
(1)求证:$\triangle ADF\backsim \triangle ACG$.
(2)若$\frac {AD}{AC}= \frac {4}{9}$,求$\frac {AF}{FG}$的值.

答案： 解析　
(1)证明:
∵∠AED=∠B,∠DAE=∠CAB,
∴△AED∽△ABC,
∴∠ADF=∠C.又
∵$\frac{AD}{AC}=\frac{DF}{CG}$,
∴△ADF∽△ACG.
(2)
∵△ADF∽△ACG,
∴$\frac{AD}{AC}=\frac{AF}{AG}$.
∵$\frac{AD}{AC}=\frac{4}{9}$,
∴$\frac{AF}{AG}=\frac{4}{9}$,又
∵AG=AF+FG,
∴$\frac{AF}{FG}=\frac{4}{5}$.