第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
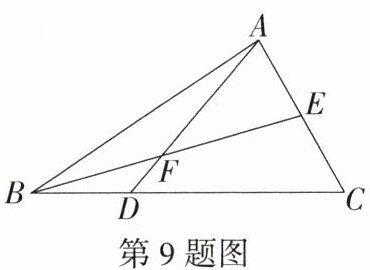
9.「2024 安徽淮北期中,」如图,$BE是\triangle ABC$的中线,点$D在BC上且满足CD = 2BD$,连接$AD$,与$BE交于点F$,则$\frac{S_{\triangle ABC}}{S_{\triangle AEF}}$的值为( )
A.$\frac{10}{3}$
B.$\frac{11}{3}$
C.4
D.$\frac{9}{2}$

A.$\frac{10}{3}$
B.$\frac{11}{3}$
C.4
D.$\frac{9}{2}$
答案:
C 如图,过点E作EG//BC交AD于G,
∴△AGE∽△ADC,
∵BE是△ABC的中线,
∴AE=EC,
∴$\frac{AE}{AC}$=$\frac{GE}{CD}$=$\frac{AG}{AD}$=$\frac{1}{2}$,
∴CD=2GE,AD=2AG,
∵CD=2BD,
∴BD=GE,
∵GE//BC,
∴∠EGF=∠BDF,
∵∠BFD=∠EFG,
∴△BDF≌△EGF(AAS),
∴DF=GF,
∴AG=2GF,设$S_{△GEF}=m$,则$S_{△AGE}=2m$,
∴$S_{△AEF}=3m$,
∵$\frac{S_{△AGE}}{S_{△ADC}}=(\frac{AE}{AC})^2=\frac{1}{4}$,
∴$S_{△ACD}=8m$,
∵CD =2BD,
∴$S_{△ABD}=4m$,
∴$S_{△ABC}=12m$,
∴$\frac{S_{△ABC}}{S_{△AEF}}$=$\frac{12m}{3m}$=4.故选C.

C 如图,过点E作EG//BC交AD于G,
∴△AGE∽△ADC,
∵BE是△ABC的中线,
∴AE=EC,
∴$\frac{AE}{AC}$=$\frac{GE}{CD}$=$\frac{AG}{AD}$=$\frac{1}{2}$,
∴CD=2GE,AD=2AG,
∵CD=2BD,
∴BD=GE,
∵GE//BC,
∴∠EGF=∠BDF,
∵∠BFD=∠EFG,
∴△BDF≌△EGF(AAS),
∴DF=GF,
∴AG=2GF,设$S_{△GEF}=m$,则$S_{△AGE}=2m$,
∴$S_{△AEF}=3m$,
∵$\frac{S_{△AGE}}{S_{△ADC}}=(\frac{AE}{AC})^2=\frac{1}{4}$,
∴$S_{△ACD}=8m$,
∵CD =2BD,
∴$S_{△ABD}=4m$,
∴$S_{△ABC}=12m$,
∴$\frac{S_{△ABC}}{S_{△AEF}}$=$\frac{12m}{3m}$=4.故选C.

10.「2023 山东日照中考,」如图,矩形$ABCD$中,$AB = 6$,$AD = 8$,点$P在对角线BD$上,过点$P作MN \perp BD$,交边$AD$,$BC于点M$,$N$,过点$M作ME \perp AD交BD于点E$,连接$EN$,$BM$,$DN$。下列结论:①$EM = EN$;②四边形$MBND$的面积不变;③当$AM:MD = 1:2$时,$S_{\triangle MPE}= \frac{96}{25}$;④$BM + MN + ND$的最小值是 20。其中所有正确结论的序号是____。


答案:
答案 ②③④
解析 ①当点N与点C重合时,可知EM≠EN,故①错误;
②如图,延长ME交BC于点H,
∵MN⊥BD,
∴∠MPD=90°,
∴∠PMD+∠PDM=90°,
∵ME⊥AD,
∴∠EMD=90°,
∴∠EMP+∠PMD=90°,
∴∠EMP=∠PDM,易知∠MHN=∠A=90°,
∴△MHN∽△DAB,
∴$\frac{MN}{BD}$=$\frac{MH}{AD}$,易得BD=10,MH=6,
∴$\frac{MN}{10}$=$\frac{6}{8}$,解得$MN=\frac{15}{2}$,
∴$S_{四边形MBND}=\frac{1}{2}×10×\frac{15}{2}=\frac{75}{2}$,故四边形MBND的面积不变,故②正确;
③当AM:MD=1:2时,易证△DME∽△DAB,
∴$\frac{ME}{AB}$=$\frac{MD}{AD}$,即$\frac{ME}{6}$=$\frac{2}{3}$,解得ME=4,易证△MPE∽△DAB,
∴$\frac{S_{△MPE}}{S_{△DAB}}=(\frac{ME}{BD})^2$,即$\frac{S_{△MPE}}{24}=(\frac{4}{10})^2$,解得$S_{△MPE}=\frac{96}{25}$,故③正确;
④如图,过点D作MN的平行线,过点M作ND的平行线,两线交于点F,连接BF,则四边形MNDF为平行四边形,
∴MF=ND,则BM+MN+ND=BM+$\frac{15}{2}$+MF,又BM+MF≥BF,故当B,M,F三点共线时,BM+MF的值最小,为BF 的长,易知BD⊥DF,$DF=MN=\frac{15}{2}$,
∴$BF=\sqrt{BD^2+DF^2}=\frac{25}{2}$,
∴BM+MN+ND的最小值为$\frac{15}{2}+\frac{25}{2}=20$,故④正确.

故正确结论的序号是②③④.
答案 ②③④
解析 ①当点N与点C重合时,可知EM≠EN,故①错误;
②如图,延长ME交BC于点H,
∵MN⊥BD,
∴∠MPD=90°,
∴∠PMD+∠PDM=90°,
∵ME⊥AD,
∴∠EMD=90°,
∴∠EMP+∠PMD=90°,
∴∠EMP=∠PDM,易知∠MHN=∠A=90°,
∴△MHN∽△DAB,
∴$\frac{MN}{BD}$=$\frac{MH}{AD}$,易得BD=10,MH=6,
∴$\frac{MN}{10}$=$\frac{6}{8}$,解得$MN=\frac{15}{2}$,
∴$S_{四边形MBND}=\frac{1}{2}×10×\frac{15}{2}=\frac{75}{2}$,故四边形MBND的面积不变,故②正确;
③当AM:MD=1:2时,易证△DME∽△DAB,
∴$\frac{ME}{AB}$=$\frac{MD}{AD}$,即$\frac{ME}{6}$=$\frac{2}{3}$,解得ME=4,易证△MPE∽△DAB,
∴$\frac{S_{△MPE}}{S_{△DAB}}=(\frac{ME}{BD})^2$,即$\frac{S_{△MPE}}{24}=(\frac{4}{10})^2$,解得$S_{△MPE}=\frac{96}{25}$,故③正确;
④如图,过点D作MN的平行线,过点M作ND的平行线,两线交于点F,连接BF,则四边形MNDF为平行四边形,
∴MF=ND,则BM+MN+ND=BM+$\frac{15}{2}$+MF,又BM+MF≥BF,故当B,M,F三点共线时,BM+MF的值最小,为BF 的长,易知BD⊥DF,$DF=MN=\frac{15}{2}$,
∴$BF=\sqrt{BD^2+DF^2}=\frac{25}{2}$,
∴BM+MN+ND的最小值为$\frac{15}{2}+\frac{25}{2}=20$,故④正确.

故正确结论的序号是②③④.
11. 教材变式「2025 安徽六安霍邱期中,」如图,$\triangle ABC$中,$AD$是高,矩形$PQMN的顶点P$,$N分别在AB$,$AC$上,$Q$,$M在BC$上,$AD交PN于点E$,$BC = 48$,$AD = 16$。
(1)若$PN = 18$,求$DE$的长。
(2)若矩形$PQMN$的周长为 80,求矩形$PQMN$的面积。

(1)若$PN = 18$,求$DE$的长。
(2)若矩形$PQMN$的周长为 80,求矩形$PQMN$的面积。

答案:
解析
(1)
∵四边形PQMN是矩形,
∴PN//QM,
∴PN//BC,
∴△APN∽△ABC,
∴$\frac{AE}{AD}$=$\frac{PN}{BC}$,设DE=x,则AE=16 - x,
∴$\frac{16 - x}{16}$=$\frac{18}{48}$,解得x=10,即DE=10.
(2)
∵四边形PQMN是矩形,AD是△ABC的高,
∴四边形PQDE为矩形,
∴DE=PQ.设DE=PQ=y,则$PN=\frac{80 - 2y}{2}=40 - y$,AE=16 - y,由
(1)知$\frac{AE}{AD}$=$\frac{PN}{BC}$,
∴$\frac{16 - y}{16}$=$\frac{40 - y}{48}$,解得y=4,
∴PN=36,
∴矩形PQMN的面积为4×36=144.
(1)
∵四边形PQMN是矩形,
∴PN//QM,
∴PN//BC,
∴△APN∽△ABC,
∴$\frac{AE}{AD}$=$\frac{PN}{BC}$,设DE=x,则AE=16 - x,
∴$\frac{16 - x}{16}$=$\frac{18}{48}$,解得x=10,即DE=10.
(2)
∵四边形PQMN是矩形,AD是△ABC的高,
∴四边形PQDE为矩形,
∴DE=PQ.设DE=PQ=y,则$PN=\frac{80 - 2y}{2}=40 - y$,AE=16 - y,由
(1)知$\frac{AE}{AD}$=$\frac{PN}{BC}$,
∴$\frac{16 - y}{16}$=$\frac{40 - y}{48}$,解得y=4,
∴PN=36,
∴矩形PQMN的面积为4×36=144.
12. 推理能力【教材呈现】沪科版九年级上册第 91 页第 6 题:
如图,$DE // BC$,且$\frac{AD}{BD}= 2$,求$\triangle ADE与\triangle ABC$的周长比。

请解答上述问题。
【应用拓展】
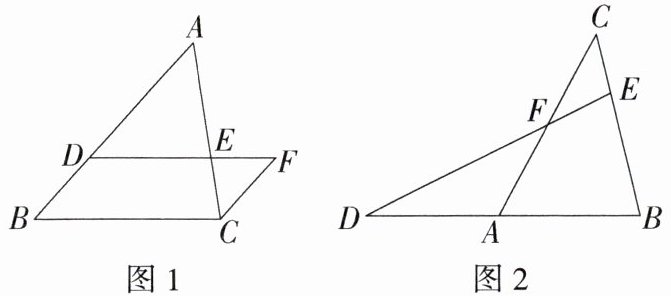
(1)如图 1,在$\triangle ABC$中,点$D在边AB$上,$DE // BC交AC于点E$。过点$C作CF // AB交DE的延长线于点F$。若$\frac{AD}{BD}= 2$,求$\triangle CEF与\triangle ABC$的周长比。
(2)如图 2,在$\triangle ABC$中,点$D为边BA$的延长线上一点,点$E为边BC$上一点,连接$DE交AC于点F$,若点$A为DB$的中点,$CE:EB = 1:2$,$\triangle DBE$的面积为 4,求$\triangle CFE$的面积。
如图,$DE // BC$,且$\frac{AD}{BD}= 2$,求$\triangle ADE与\triangle ABC$的周长比。

请解答上述问题。
【应用拓展】
(1)如图 1,在$\triangle ABC$中,点$D在边AB$上,$DE // BC交AC于点E$。过点$C作CF // AB交DE的延长线于点F$。若$\frac{AD}{BD}= 2$,求$\triangle CEF与\triangle ABC$的周长比。
(2)如图 2,在$\triangle ABC$中,点$D为边BA$的延长线上一点,点$E为边BC$上一点,连接$DE交AC于点F$,若点$A为DB$的中点,$CE:EB = 1:2$,$\triangle DBE$的面积为 4,求$\triangle CFE$的面积。

答案:
解析 [教材呈现]
∵DE//BC,
∴△ADE∽△ABC.
∵$\frac{AD}{BD}=2$,
∴$\frac{AD}{AB}=\frac{2}{3}$,
∴$\frac{△ADE的周长}{△ABC的周长}=\frac{2}{3}$.
[应用拓展]
(1)由[教材呈现],可知$\frac{△ADE的周长}{△ABC的周长}=\frac{2}{3}$.
∵DE//BC,
∴$\frac{CE}{AE}$=$\frac{BD}{AD}$=$\frac{1}{2}$,
∵CF//AB,
∴△CEF∽△AED,
∴$\frac{△CEF的周长}{△ADE的周长}=\frac{CE}{AE}=\frac{1}{2}$,
∴$\frac{△CEF的周长}{△ABC的周长}=\frac{1}{3}$
(2)如图,过点A作AG//DE,交BE于点G,
∴△BAG ∽△BDE,
∵点A为DB的中点,
∴$\frac{AB}{BD}$=$\frac{BG}{BE}$=$\frac{1}{2}$,
∵CE:EB=1:2,
∴BG=CE=EG,
∵△DBE的面积为4,
∴△ABG的面积为1,
∴△ACG的面积为2,
∵AG//EF,
∴△CFE∽△CAG,$\frac{S_{△CFE}}{S_{△CAG}}=(\frac{CE}{CG})^2=\frac{1}{4}$,即$\frac{S_{△CFE}}{2}=\frac{1}{4}$,
∴△CFE的面积为$\frac{1}{2}$.

解析 [教材呈现]
∵DE//BC,
∴△ADE∽△ABC.
∵$\frac{AD}{BD}=2$,
∴$\frac{AD}{AB}=\frac{2}{3}$,
∴$\frac{△ADE的周长}{△ABC的周长}=\frac{2}{3}$.
[应用拓展]
(1)由[教材呈现],可知$\frac{△ADE的周长}{△ABC的周长}=\frac{2}{3}$.
∵DE//BC,
∴$\frac{CE}{AE}$=$\frac{BD}{AD}$=$\frac{1}{2}$,
∵CF//AB,
∴△CEF∽△AED,
∴$\frac{△CEF的周长}{△ADE的周长}=\frac{CE}{AE}=\frac{1}{2}$,
∴$\frac{△CEF的周长}{△ABC的周长}=\frac{1}{3}$
(2)如图,过点A作AG//DE,交BE于点G,
∴△BAG ∽△BDE,
∵点A为DB的中点,
∴$\frac{AB}{BD}$=$\frac{BG}{BE}$=$\frac{1}{2}$,
∵CE:EB=1:2,
∴BG=CE=EG,
∵△DBE的面积为4,
∴△ABG的面积为1,
∴△ACG的面积为2,
∵AG//EF,
∴△CFE∽△CAG,$\frac{S_{△CFE}}{S_{△CAG}}=(\frac{CE}{CG})^2=\frac{1}{4}$,即$\frac{S_{△CFE}}{2}=\frac{1}{4}$,
∴△CFE的面积为$\frac{1}{2}$.

查看更多完整答案,请扫码查看


